貝式定理
假設有一個抽獎箱內有紅球與藍球,球上有標示 A 與 B 類別。 $$ \begin{array}{|c|c|} \hline A&B\\\hline \blue{\text{●}}\blue{\text{●}}\blue{\text{●}}\red{\text{●}}&\blue{\text{●}}\blue{\text{●}}\red{\text{●}}\red{\text{●}}\red{\text{●}}\red{\text{●}}\\\hline \end{array} $$
- 我們抽到藍球,它是來自於 A 的機率為何,即求 \(P(A|\blue{\text{●}})\)?
根據貝式定理: $$ P(A|x)=\frac{P(x|A)P(A)}{P(x|A)P(A)+P(x|B)P(B)} $$
- 先驗機率
- \(P(A)=\frac{\text{A的球數}}{\text{總球數}}=\frac{4}{10}\)
- \(P(B)=\frac{\text{B的球數}}{\text{總球數}}=\frac{6}{10}\)
- 條件機率
- \(P(\blue{\text{●}}|A)=\frac{\text{A中的}\blue{\text{●}}}{\text{A的總球數}}=\frac{3}{4}\)
- \(P(\blue{\text{●}}|B)=\frac{\text{B中的}\blue{\text{●}}}{\text{B的總球數}}=\frac{2}{6}\) 套入公式可得 $$ P(A|\blue{\text{●}})=\frac{P(\blue{\text{●}}|A)P(A)}{P(\blue{\text{●}}|A)P(A)+P(\blue{\text{●}}|B)P(B)}=\frac{3/4\times4/10}{3/4\times4/10+2/6\times6/10}=\frac{3}{5} $$
- 假設今天猜中類別才能得獎,已經知道是藍球的情況下,來自 A 的機率是 0.6,來自 B 的機率是 0.4,所以我們理論上會選擇 A,因為機率較大。換言之,在機器學習中,我們判斷一個二元分類的問題,我們會將分類判給機率 > 0.5 的那個類別。
- 先驗機率
高斯分布
- 一維的高斯分分機率密度函數(probability density function, pdf)為:
$$
f_{\mu,\sigma}(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp\bigg\lbrace-\frac{(x-\mu)^2}{2\sigma^2}\bigg\rbrace
$$
- 其中
- \(\mu\) 為平均數(Mean),決定分布的中心位置。
- \(\sigma\) 為標準差(Standard Deviation),決定分布的寬度。
- 其中
- 擴展到 n 維向量的多維高斯分布機率密度函數為:
$$
f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp\bigg\lbrace-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\bigg\rbrace
$$
其中 x 是一階張量 $$ x = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} $$
\(\mu\) 代表 x 在每個維度的均值 $$ \mu = \begin{bmatrix} \mu_1 \\ \mu_2 \\ \vdots \\ \mu_n \end{bmatrix} $$
\(\Sigma\) 是協方差矩陣,\(\Sigma\in\mathbb{R}^{n \times n}\),表示數據分布的相關性與變異性: $$ \Sigma = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \cdots & \sigma_{1n} \\ \sigma_{21} & \sigma_{22} & \cdots & \sigma_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{n1} & \sigma_{n2} & \cdots & \sigma_{nn} \end{bmatrix} $$
\(|\Sigma|\)是協方差矩陣的行列式,表示協方差矩陣的尺度,用於歸一化分布。
\(\Sigma^{-1}\)是協方差矩陣的逆矩陣,用於計算標準化的二次型距離。
\((x - \mu)^T \Sigma^{-1} (x - \mu)\)是馬氏距離(Mahalanobis Distance),表示點 \(x\) 與均值 \(\mu\) 的加權距離。
二元分類
我們嘗試使用高斯分布模型對一個簡單的問題進行描述:
- 假設我們想用身高、體重來猜測一個人的性別:
class HeightWeightGenerator: def __init__(self): # 設定男性身高體重的均值和協方差 self.male_mean = np.array([172, 70]) # [height, weight] self.male_cov = np.array([[60, 20], # height與weight的協方差矩陣 [20, 35]]) # 設定女性身高體重的均值和協方差 self.female_mean = np.array([162, 55]) self.female_cov = np.array([[35, 15], [15, 20]]) def generate_samples(self, n_samples=1000): # 生成性別 (0: 女性, 1: 男性) genders = np.random.binomial(n=1, p=0.5, size=n_samples) # 初始化數據陣列 data = np.zeros((n_samples, 2)) # 生成男性和女性的身高體重數據 male_indices = genders == 1 female_indices = genders == 0 # 使用多維高斯分布生成數據 data[male_indices] = np.random.multivariate_normal( self.male_mean, self.male_cov, size=np.sum(male_indices)) data[female_indices] = np.random.multivariate_normal( self.female_mean, self.female_cov, size=np.sum(female_indices)) return data, genders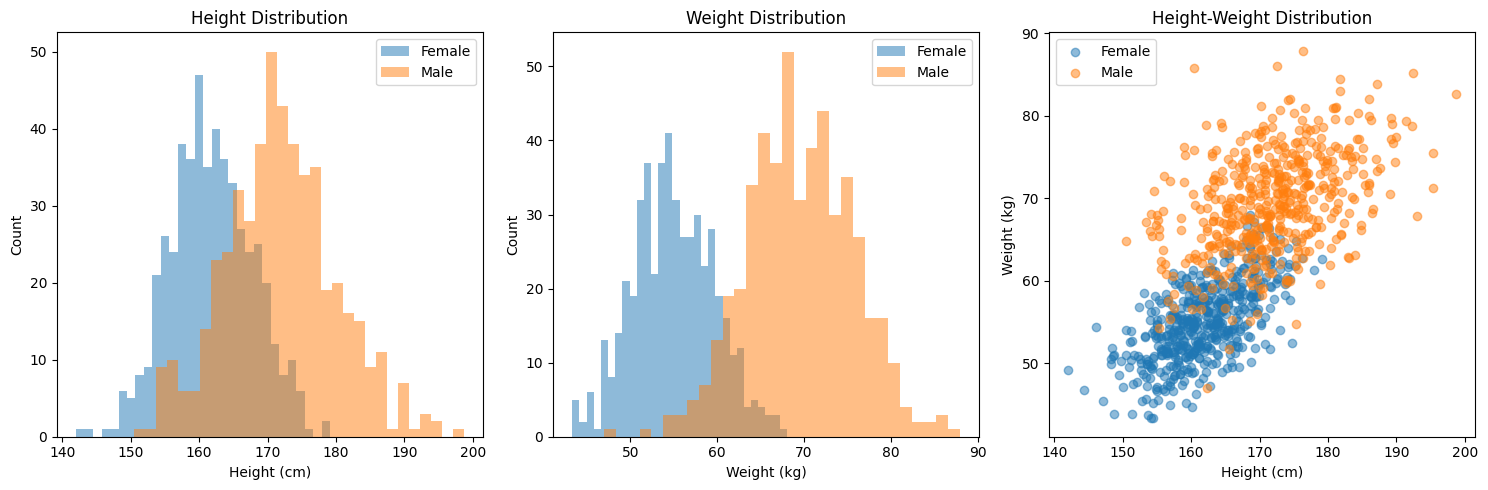
- 假設
- \(x = [\text{身高}, \text{體重}]^T \in \mathbb{R}^2\):每個數據點的特徵向量。
- 類別 \(y \in {0,要 1}\):性別標籤,0 表示女,1 表示男。
基本假設
高斯分布假設
- \(P(x|y=0) \sim \mathcal{N}(\mu_0, \Sigma_0)\):女生特徵的高斯分布。
- \(P(x|y=1) \sim \mathcal{N}(\mu_1, \Sigma_1)\):男生特徵的高斯分布。
目標
- 利用貝氏定理計算 \(P(y|x)\): $$ P(y|x) = \frac{P(x|y)P(y)}{P(x)} $$
- 其中:
- \(P(x|y)\):由高斯分布表示。
- \(P(y)\):類別的先驗概率(例如, \(P(y=1)\) 和 \(P(y=0)\) 可以從訓練數據中估計)。
- \(P(x)\):由所有類別的加權概率總和給出。
輸出
- 使用 \(P(y=1|x)\) 作為預測為男的概率,並通過交叉熵損失來進行模型訓練。
代入高斯分布機率密度函數
- 條件概率 \(P(y|x)\)
由於 \(P(x)\) 是常數,實際上只需要比較 \(P(x|y)P(y)\) 即可: $$ P(y=1|x) = \frac{P(x|y=1)P(y=1)}{P(x|y=1)P(y=1) + P(x|y=0)P(y=0)} $$
將 \(P(x|y)\) 展開為高斯分布: $$ P(x|y=k) = \frac{1}{(2\pi)^{n/2} |\Sigma_k|^{1/2}} \exp\left(-\frac{1}{2}(x - \mu_k)^T \Sigma_k^{-1} (x - \mu_k)\right), \quad k \in {0, 1} $$
預測概率 定義 \(h(x)\) 為模型的預測概率: $$ h(x) = P(y=1|x) = f(\mu,\Sigma) $$
- 換言之我們的模型是一個 \(f(\mu,\Sigma)\),以 \(\mu\) 與 \(\Sigma\) 為參數的模型。
損失函數 使用交叉熵損失(BCE, binary crossentropy): $$ L = -\frac{1}{m} \sum_{i=1}^m \left[ y_i \log(h(x_i)) + (1 - y_i) \log(1 - h(x_i)) \right], $$ 其中:
- \(h(x_i)\):由高斯分布計算出的 \(P(y=1|x_i)\)。
- \(y_i\):訓練數據的真實標籤。
class GaussianClassifier: def __init__(self, shared_sigma=False): self.shared_sigma = shared_sigma def fit(self, X, y, lr=0.01, epochs=100): # 初始化參數 self.mu_0 = np.mean(X[y==0], axis=0) # class 0 的均值 self.mu_1 = np.mean(X[y==1], axis=0) # class 1 的均值 if self.shared_sigma: # 使用共用的協方差矩陣 self.sigma = np.cov(X.T) else: # 分別計算每個類別的協方差矩陣 self.sigma_0 = np.cov(X[y==0].T) self.sigma_1 = np.cov(X[y==1].T) self.losses = [] # 梯度下降 for _ in tqdm(range(epochs)): # 計算每個類別的概率 if self.shared_sigma: p_0 = multivariate_normal.pdf(X, self.mu_0, self.sigma) p_1 = multivariate_normal.pdf(X, self.mu_1, self.sigma) else: p_0 = multivariate_normal.pdf(X, self.mu_0, self.sigma_0) p_1 = multivariate_normal.pdf(X, self.mu_1, self.sigma_1) # 計算後驗概率 p = p_1 / (p_0 + p_1) # 計算BCE損失 loss = -np.mean(y * np.log(p + 1e-15) + (1-y) * np.log(1 - p + 1e-15)) self.losses.append(loss) # 計算梯度並更新參數 for i in range(len(X)): diff_0 = X[i] - self.mu_0 diff_1 = X[i] - self.mu_1 if self.shared_sigma: inv_sigma = np.linalg.inv(self.sigma) if y[i] == 0: self.mu_0 += lr * inv_sigma.dot(diff_0) self.sigma += lr * (np.outer(diff_0, diff_0).dot(inv_sigma) - inv_sigma) else: self.mu_1 += lr * inv_sigma.dot(diff_1) self.sigma += lr * (np.outer(diff_1, diff_1).dot(inv_sigma) - inv_sigma) # 確保協方差矩陣是正定的 self.sigma = (self.sigma + self.sigma.T) / 2 eigvals = np.linalg.eigvals(self.sigma) if np.any(eigvals < 0): self.sigma += np.eye(2) * (abs(min(eigvals)) + 1e-6) else: if y[i] == 0: inv_sigma_0 = np.linalg.inv(self.sigma_0) self.mu_0 += lr * inv_sigma_0.dot(diff_0) self.sigma_0 += lr * (np.outer(diff_0, diff_0).dot(inv_sigma_0) - inv_sigma_0) self.sigma_0 = (self.sigma_0 + self.sigma_0.T) / 2 else: inv_sigma_1 = np.linalg.inv(self.sigma_1) self.mu_1 += lr * inv_sigma_1.dot(diff_1) self.sigma_1 += lr * (np.outer(diff_1, diff_1).dot(inv_sigma_1) - inv_sigma_1) self.sigma_1 = (self.sigma_1 + self.sigma_1.T) / 2 def predict(self, X): if self.shared_sigma: p_0 = multivariate_normal.pdf(X, self.mu_0, self.sigma) p_1 = multivariate_normal.pdf(X, self.mu_1, self.sigma) else: p_0 = multivariate_normal.pdf(X, self.mu_0, self.sigma_0) p_1 = multivariate_normal.pdf(X, self.mu_1, self.sigma_1) return (p_1 > p_0).astype(int)- 我用了兩個策略,一個是各別計算協方差矩陣(左),一個是共用協方差矩陣(右)。
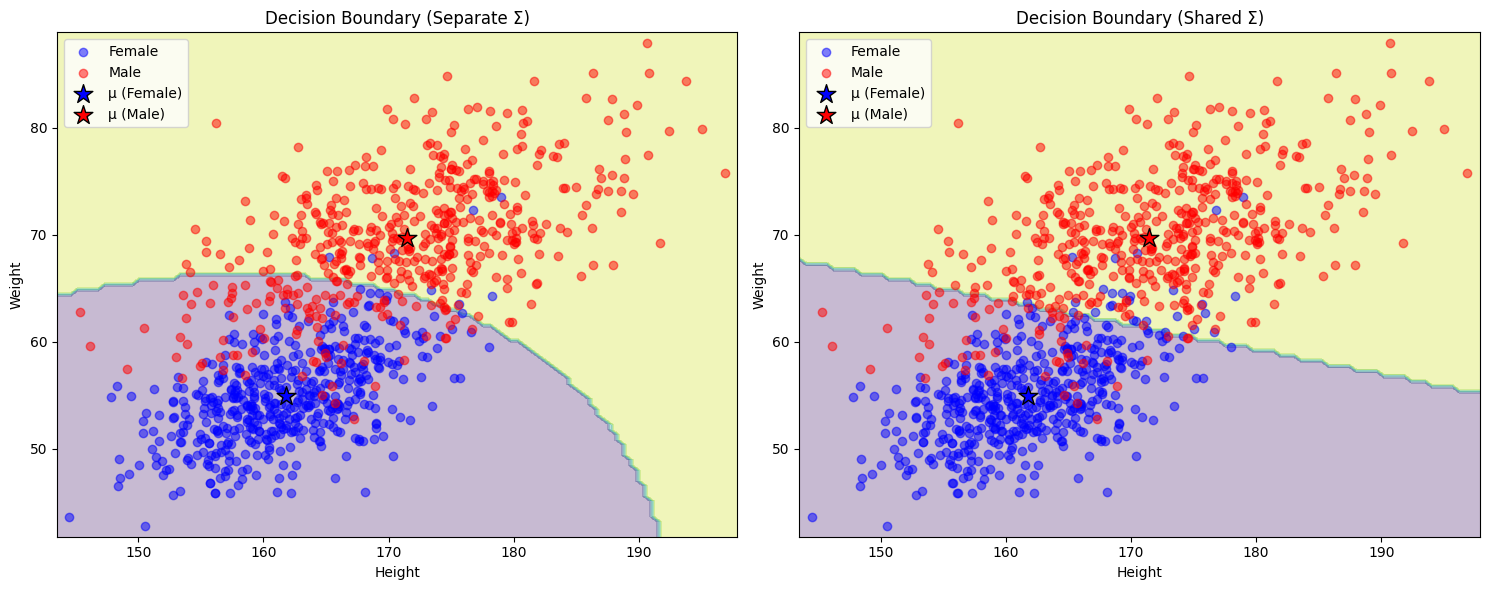
- 優缺點:
分離Σ的優勢:
- 更好地捕捉每個類別的特徵
- 可以處理類別有不同形狀的情況
共用Σ的優勢:(boundary 會是線性的)
- 參數更少,不容易過擬合
- 計算更高效
- 決策邊界更簡單
- **摘要:**數據量較小或類別分布相似,建議使用共用Σ的模型;如果數據量大且類別分布差異明顯,可以考慮使用分離Σ的模型。
- 條件概率 \(P(y|x)\)
Sigmoid ?
- 若所有維度都是非相關的,我們可以使用 Naive Bayes Classifier
- 則後設計率為 $$ P(A|x)=\frac{P(x|A)P(A)}{P(x|A)P(A)+P(x|B)P(B)}=\frac{1}{1+\frac{P(x|B)P(B)}{P(x|A)P(A)}} $$
- 令 \(z=\ln\frac{P(x|A)P(A)}{P(x|B)P(B)}\),則 $$ P(A|x)=\frac{1}{1+exp(-z)}=\sigma(z) $$
- 哈,是 sigmoid 函式! $$ z=\ln\frac{P(x|A)P(A)}{P(x|B)P(B)}=\ln\frac{P(x|A)}{P(x|B)}+\ln\frac{P(A)}{P(B)} $$
- 後面的這一項,可以從訓練資料得到 \(\frac{P(A)}{P(B)}=\frac{N_A}{N_B}\) $$ P(x|A)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma_A|^{1/2}}exp\bigg\lbrace{-\frac{1}{2}(x-\mu_A)^T(\Sigma_A)^{-1}(x-\mu_A)}\bigg\rbrace\\ P(x|B)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma_B|^{1/2}}exp\bigg\lbrace{-\frac{1}{2}(x-\mu_B)^T(\Sigma_B)^{-1}(x-\mu_B)}\bigg\rbrace $$ $$ z=\ln\frac{N_A}{N_B}+\frac{\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma_A|^{1/2}}exp\bigg\lbrace{-\frac{1}{2}(x-\mu_A)^T(\Sigma_A)^{-1}(x-\mu_A)}\bigg\rbrace}{\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma_B|^{1/2}}exp\bigg\lbrace{-\frac{1}{2}(x-\mu_B)^T(\Sigma_B)^{-1}(x-\mu_B)}\bigg\rbrace} $$ $$ z=\ln\frac{N_A}{N_B}+\ln\frac{|\Sigma_B|^{1/2}}{|\Sigma_A|^{1/2}}exp\bigg\lbrace{-\frac{1}{2}[(x-\mu_A)^T(\Sigma_A)^{-1}(x-\mu_A)-(x-\mu_B)^T(\Sigma_B)^{-1}(x-\mu_B)]}\bigg\rbrace $$ $$ z=(\mu_A-\mu_B)^T\Sigma^{-1}\red{x}-\frac{1}{2}(\mu_A)^T(\Sigma_A)^{-1}\mu_A+\frac{1}{2}(\mu_B)^T(\Sigma_B)^{-1}\mu_B+\ln\frac{N_A}{N_B} $$
- 發現酷東西了: $$ z=w^Tx+b $$
- 將 z 代入原式 $$ P(A|x)=\sigma(z)=\sigma(w\cdot x+b) $$
- 換言之,我們透過求 \(N_A, N_B, \mu_A, \mu_B, \Sigma \) 可以得到 w, b
- 那我們是不是可以假設 \(f(y)=\sigma(wx+b)\),直接求 \(w^* \)與 \( b^*\)
Crossentropy?
- 百努力分布(Bernoulli Distribution)寫成,其中 k = 0 或 1 $$ P(x=k)=p^k\times(1-p)^{(1-k)} $$
- 假設我們的 \(y\) 滿足百努力分布,則模型的輸出 \(\hat{y}\) 可視為對 p 的估計,我們可以將損失函數寫成 $$ L(w,b)=f_{w,b}(x_1)f_{w,b}(x_2)(1-f_{w,b}(x_3))\cdots f_{w,b}(x_n) $$
- 同取 ln $$ \ln L(w,b)=\sum_{i=1}^n [y_i\ln f_{w,b}(x_i)+(1-y_i)\ln(1-f_{w,b}(x_i))] $$
- 為了使其最小化,我們取負號,得到交叉熵損失函數: $$ J(w,b)=-\frac{1}{n}\sum_{i=1}^n [y_i\ln f_{w,b}(x_i)+(1-y_i)\ln(1-f_{w,b}(x_i))] $$
- 其中:
- \(y_i\) 是第 i 個樣本的真實標籤(0或1)
- \(f_{w,b}(x_i)\) 是模型對第 i 個樣本的預測值(介於0和1之間)
- \(\frac{1}{n}\) 是為了取平均
二元分類 v.s. 線性迴歸
$$ \begin{array}{c|c|c} &\text{Logistic Regression}&\text{Linear Regression}\\\hline \text{function}&f_{w,b}(x)=\sigma(\sum_i w_ix_i+b)&f_{w,b}(x)=\sum_i w_ix_i+b\\\hline \text{loss function}&L(f)=\sum_iC(f(x_i),\hat{y}_i)&L(f)=\frac{1}{2}\sum_i(f(x_i)-\hat{y}_i)^2\\\hline \text{update}&w_i=w_i-\eta\sum_i (f(x_i)-\hat{y}_i)x_i&w_i=w_i-\eta\sum_i (f(x_i)-\hat{y}_i)x_i\\ \end{array} $$
- 可以發現 Linear Regression 與 Logistic Regression 基本上是差不多的作法,差別是 Logistic 使用了 sigmoid function,在 loss function 的部分使用了二元交叉熵。
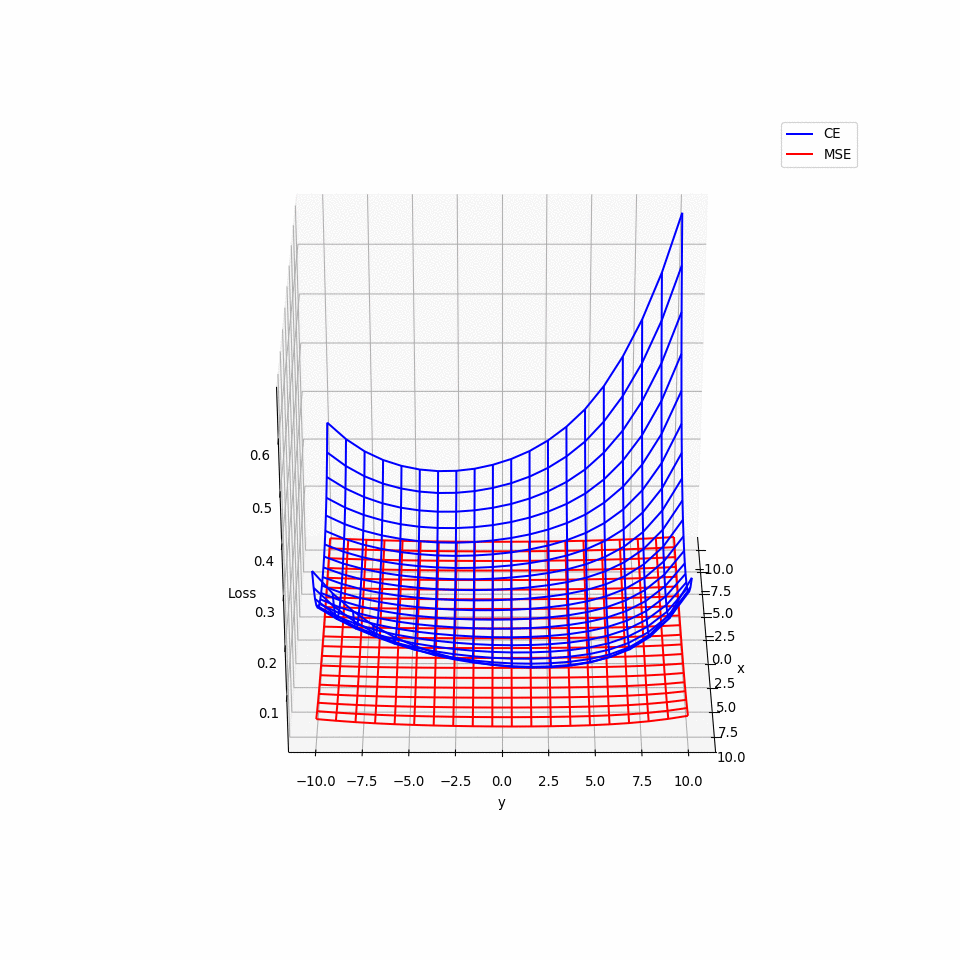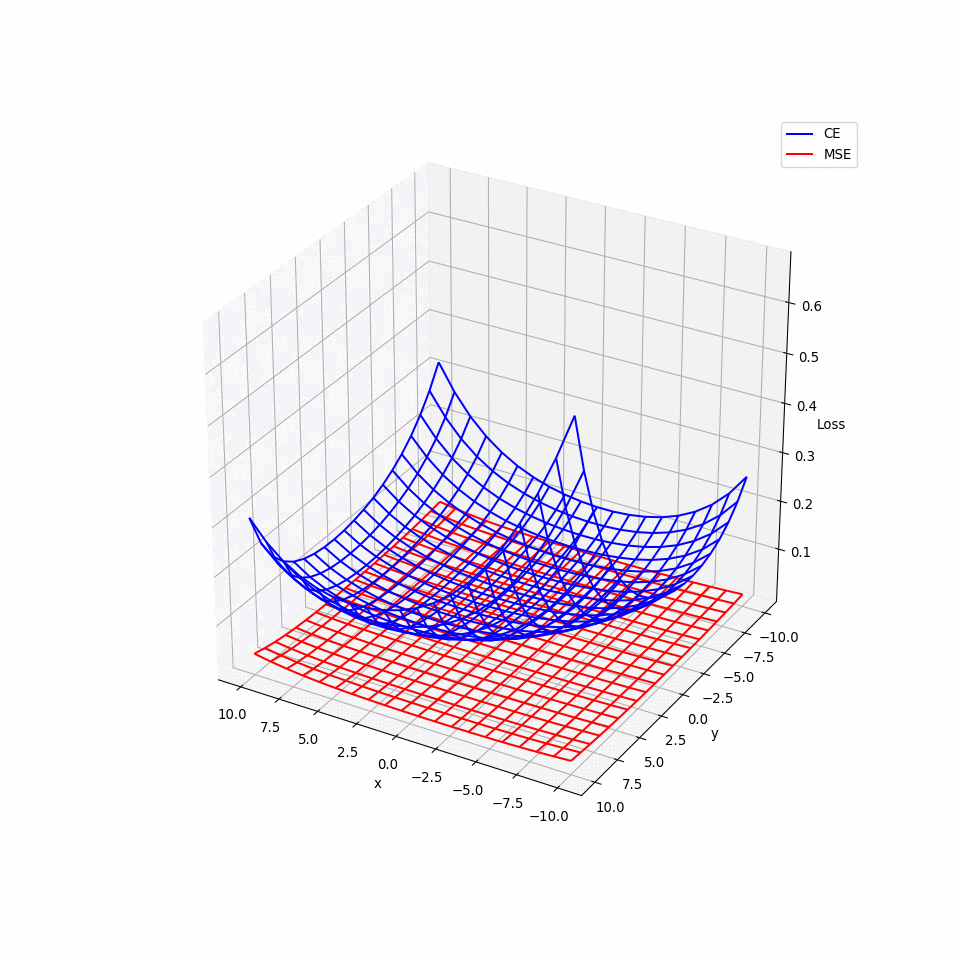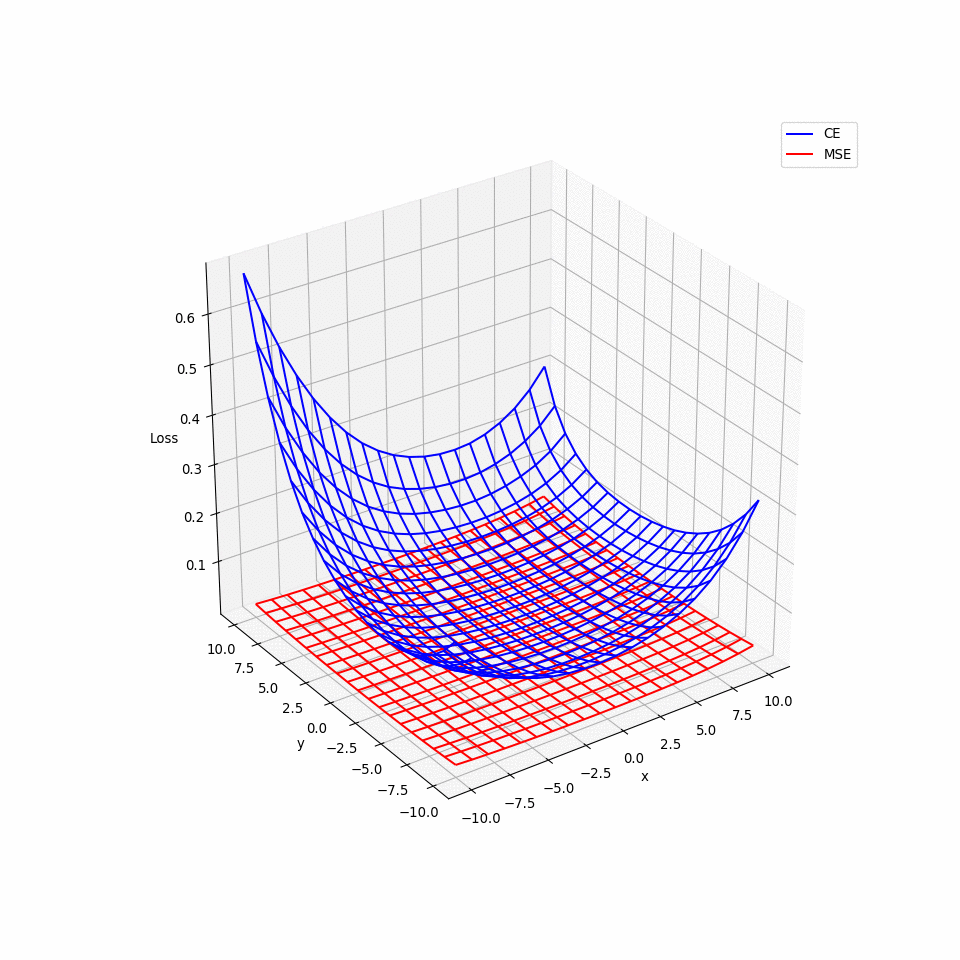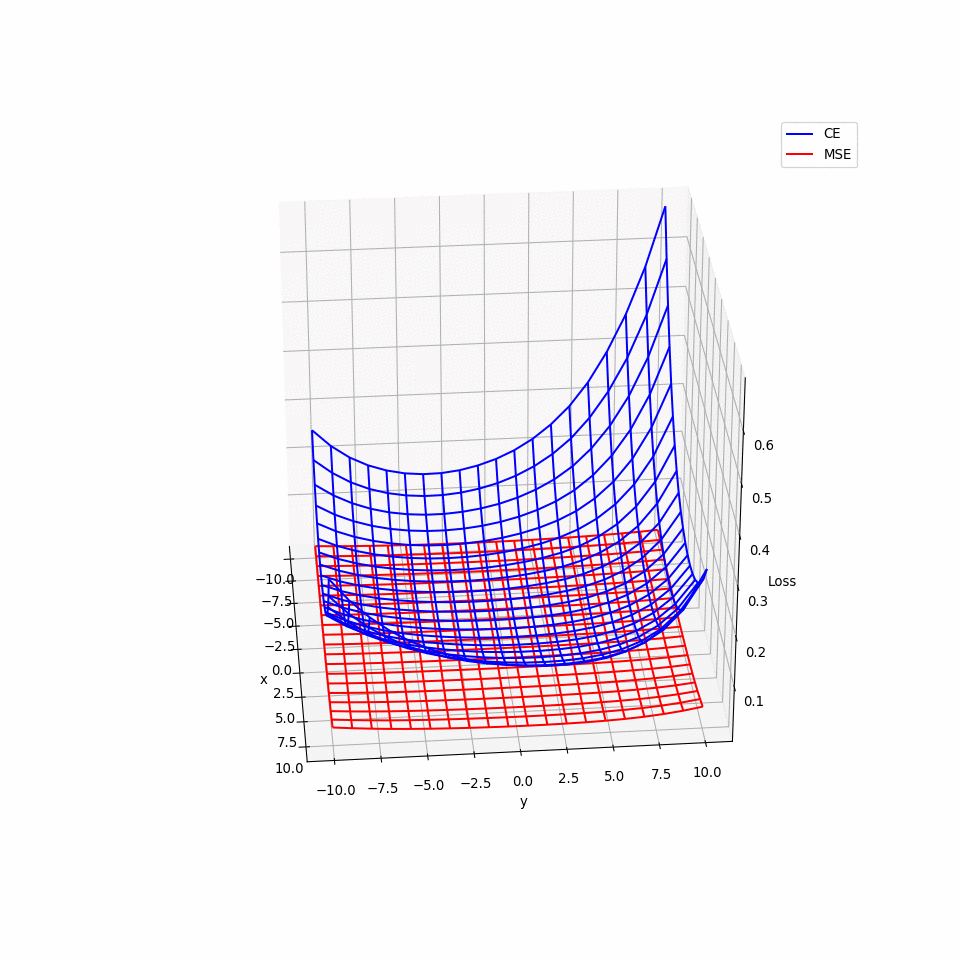
- 那為何 Logistic Regression 不使用 MSE 呢? 用微分會發現 $$ \frac{\partial L(f)}{\partial w_i}=2(f_{w,b}(x)-\hat{y}f_{w,b}(x)(1-f_{w,b}(x)))x_i $$
- \(\hat{y}_i=0或1\),在 \(f(x_i)=0或1\)時,\(\frac{\partial L}{\partial w_i}皆=0\),換言之在接近 target,與相當遠離 target 的地方,梯度都為 0,也就是說使用 MSE 會有梯度遺失的問題。
Discriminative v.s. Generative
- 我們先前採用高斯模型,並透過找尋最佳的 \(\mu\) 與 \(\Sigma\) 來找到最佳的高斯分布密度方程式的方法稱為 Generative,那既然我們發現其實
$$
z=(\mu_A-\mu_B)^T\Sigma^{-1}\red{x}-\frac{1}{2}(\mu_A)^T(\Sigma_A)^{-1}\mu_A+\frac{1}{2}(\mu_B)^T(\Sigma_B)^{-1}\mu_B+\ln\frac{N_A}{N_B}
$$
符合了 \(z=w^Tx+b\) 的 pattern,那能否直接代入
wx+b來求最佳的 \(w\) 與 \(b\) 呢?答案是可以的,這種方法就稱為 Discriminative 的方法。 - 那這兩種方法求出來的方程式會一樣嗎?答案是不一樣。主要原因在於這兩種方法的目標函數(objective function)不同:
- 判別式方法(Discriminative):
- 直接學習後驗機率 P(y|x)
- 目標函數是最大化條件似然(conditional likelihood)
- 損失函數通常是交叉熵(cross entropy)或負對數似然
- 只關注如何根據輸入特徵x預測類別y
- 生成式方法(Generative):
- 學習聯合機率分布 P(x,y) = P(x|y)P(y)
- 目標函數是最大化聯合似然(joint likelihood)
- 需要同時建模特徵的分布P(x|y)和類別的先驗機率P(y)
- 不僅要預測y,還要能夠"生成"符合該類別的特徵x
- 判別式方法(Discriminative):
- 一般來說:
- 當訓練數據充足時,判別式模型表現較好,因為它直接優化分類效果
- 當訓練數據較少時,生成式模型可能表現更好,因為它對數據分布有更強的假設
- 需要注意的是,這兩種方法的參數更新規則和收斂性質也會不同,因此即使使用相同的學習率和初始值,最終得到的結果也會有所差異。
Logistic Regression 的限制
- 並不能表示所有的情況,例如 xor gate。
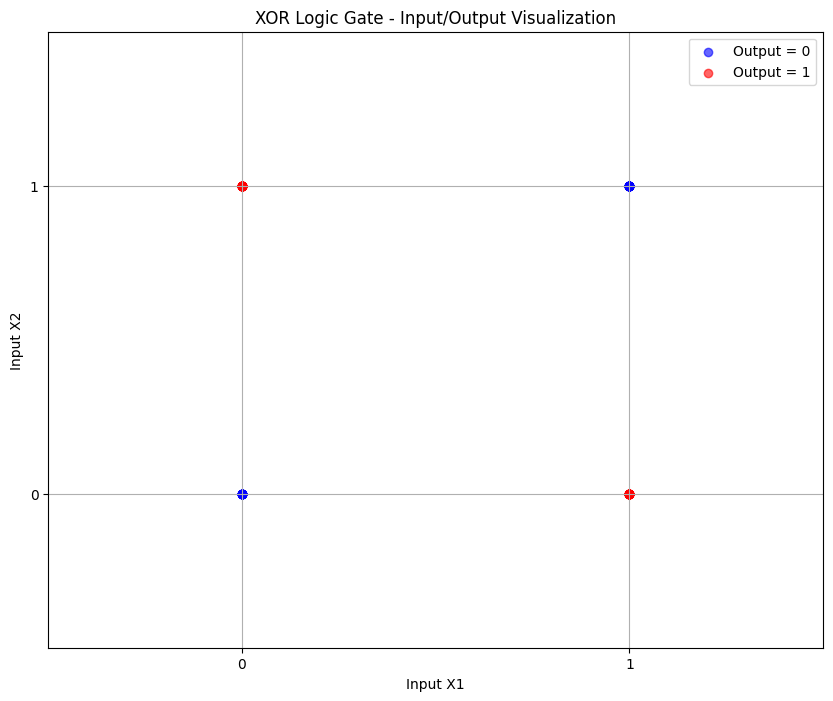
- 因為我們無法找到一個線性模型來有效的描述 xor gate。
- 在這種情況下,我們需要嘗試做 Feature Transformation,將 xor gate 的 input & output 做特殊的轉換,使線性模型可以描述
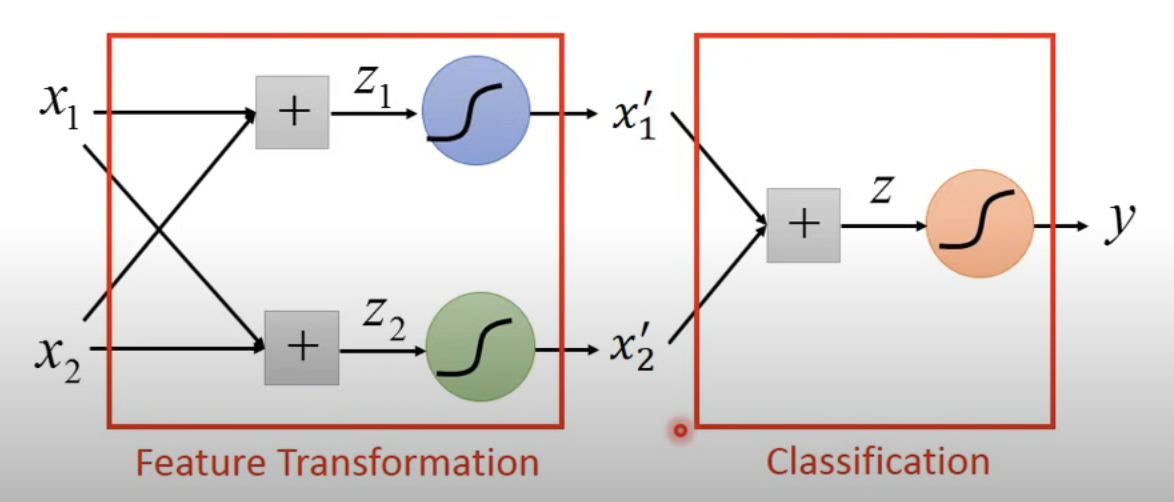
- 事實上這種作法就是在 output layer 前,加一個 hidden layer 作 feature transformation。一個\(z=\sigma(wx_i+b)\) 被我們稱為一個 neural node,由一群 neural node 組成的模型,即稱為 neural network。