一、分治法

  • 分治法，簡而言之就是分而治之，把複雜的問題分成兩個或更多個相似或相似的子問題，直到子問題可以直接求解，最後再將子問題的解做合併。
  • 三步驟：Divide、Conquer、Merge
  • 以 pseudo code 來表示大概像：
    void func(collection set) {
    // 子問題求解
    if (base_case) {
        // 根據要求將子問題解合併成母問題解
        do_something
        return;
    }
    // 將母問題分解成子問題
    for (collection subset : set) {
        func(subset);
    }
}
graph LR; 母問題-->子問題1; 母問題-->子問題2; subgraph Divide 子問題1-->最小子問題1; 子問題1-->最小子問題2; 子問題2-->最小子問題3; 子問題2-->最小子問題4; end subgraph Conquer 最小子問題1-->最小子問題解1; 最小子問題2-->最小子問題解2; 最小子問題3-->最小子問題解3; 最小子問題4-->最小子問題解4; end subgraph Merge 最小子問題解1-->合併; 最小子問題解2-->合併; 最小子問題解3-->合併; 最小子問題解4-->合併; end 合併-->母問題解
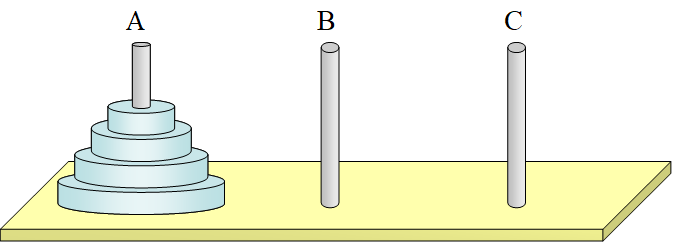
  • 舉例說明，河內塔遊戲： hanoi
    • 河內塔是由三根桿子以大小不同碟片所組成的遊戲，僧人一次可以從一根桿子移動一個碟片到另一根桿子，但是小的碟片若放憂大的碟片下面會使得小的碟片裂開(也就是碟片只能由上而下從小排到大)，試問將一座塔從一根桿子完整的移動到另一根桿子需要移動多少次。 solve
    • 思考上面的情形，以三個碟片為例，若我們要從 A 到 C 移動一座塔，我們可以將之分解成「如何把上面兩個碟片移動到 B」，因為剩下的一個大碟片，可以很簡單的從 A 移動到 C。也就是說 f3(A->C) = f2(A->B) + f1(A->C) + f2(B->C)。
    • 再更進一步，f2(A->B) 和 f2(B->C) 其實就是移動兩個碟片到另一座塔，所以可以分解成 f2(A->C) = f1(A->B) + f1(A->C) + f1(B->C)，至此，我們已經把 f3 都分解成可以代表一次移動的最小子問題的解 f1 了：
      graph TD; A[f3,A->C] B[f2,A->B] C[f1,A->C] D[f2,B->C] E[f1,A->C] F[f1,A->B] G[f1,C->B] H[f1,B->A] I[f1,B->C] J[f1,A->C] A-->B A--->C A-->D B-->E B-->F B-->G D-->H D-->I D-->J
    • 故我們可以以數學方式證明：
      \(\begin{array}{l} T(n)=T(n-1)+T(1)+T(n-1)=2T(n-1)+T(1)\\ T(n-1)=T(n-2)+T(1)+T(n-2)=2T(n-2)+T(1)\\ T(n)=2[2T(n-2)+T(1)]+T(1)\\ T(n)=2\times2T(n-2)+(1+2)T(1)\\ T(n)=2^k\times T(n-k)+(1+2+…+2^k)T(1)\\ 令k=n-1\\ T(n)=2^{n-1}\times T(1)+(1+2+…+2^{n-1})T(1)\\ T(n)=2^{n-1}\times T(1)+\frac{2^{n-1}-1}{2-1}T(1)\\ T(n)=(2^n-1)\times T(1) \end{array}\)
    • 得所需要的移動次數為 \(2^n-1\) 次
  • 分治法的特色
    1. 要解決的問題有一定的規模
    2. 該問題可以分解成若干個規模較小的問題
    3. 可以找到一個 base case，可以直接求解(如上述數學證明的\(T(1)\))
    4. 分解出來的子問題都是相互獨立的。(若有相依性，則無法使用分治法)
  • 分治法的時間複雜度
    • 將規模為 n 的問題分為 k個規模為 n/m 的子問題去解，那麼可以得到
      \(T(n)=kT(n/m)+f(n)\)

二、分治法的應用

  • 令有一已排序的數列，欲查找該數列中是否有數值 x。
    • 由於該數列已經過排序，所以我們無需遍歷整個數列，我們可以選擇每次挑選數列的中間值，若目標比中間值大，則選擇大的那側再繼續做篩選，此法稱為二元搜索法，其時間複雜度可以從線性搜索法的 \(O(n)\) 降低到 \(O(n\log n)\)。
    int binarySearch(vector<int>& nums, int target) {
    int left = 0, right = nums.size()-1;
    while (left <= right) {
        int mid = left + (right-left)/2;
        if (nums[mid] == target)
            return mid;
        else if (nums[mid] < target) 
            left = mid + 1;
        else if (nums[mid] > target)
            right = mid - 1;
    }
    return -1;
}

2. Strassen 矩陣乘法

  • 試做一個矩陣\(A\)與矩陣\(B\)內積。
    • \( A=\left[\begin{matrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{matrix}\right], B=\left[\begin{matrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{matrix}\right], C=\left[\begin{matrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{matrix}\right],其中\\ \left[\begin{matrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{matrix}\right]=\left[\begin{matrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{matrix}\right]\cdot\left[\begin{matrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{matrix}\right] \)
    • 若通過一般展開可得
      \( C_{11}=A_{11}\cdot B_{11}+A_{12}\cdot B_{21}\\ C_{12}=A_{11}\cdot B_{12}+A_{12}\cdot B_{22}\\ C_{21}=A_{21}\cdot B_{11}+A_{22}\cdot B_{21}\\ C_{22}=A_{21}\cdot B_{12}+A_{22}\cdot B_{22} \)
    • 從上可得計算兩個 \(n\cdot n\) 的矩陣內積需要 兩個 \(\frac{n}{2}\cdot\frac{n}{2}\) 的矩陣做 8 次的乘法加上 4 次的加法，其時間複雜度可以表示成：
      • \( T(n)=8T(\frac{n}{2})+\Theta(n^2)\\ T(\frac{n}{2})=8T(\frac{n}{4})+\Theta({\frac{n}{2}}^2)\\ T(n)=8\left[{8T(\frac{n}{4})+\Theta({{(\frac{n}{2}})}^2)}\right]+\Theta(n^2)\\ T(n)=8^2T(\frac{n}{4})+\Theta(n^2)+8\Theta(\frac{n^2}{4})=8^2T(\frac{n}{4})+(1+2)\Theta(n^2)\\ T(n)=8^kT(\frac{n}{2^k})+(1+2+…+2^{k-1})\Theta(n^2)\\ 令n=2^k\\ T(n)=n^3T(1)+(\frac{n/2-1}{2-1})\Theta(n^2)\approx \Theta(n^3) \)
    • 若使用 Strassen 演算法
      1. 同樣將矩陣\(A,B,C\)作分解，\(時間\Theta(1)\)
      2. 創建 10 個 \(\frac{n}{2}\cdot\frac{n}{2}\) 的矩陣 \(S_1,S_2,…,S_{10}\)，時間\(\Theta(n^2)\)
        \( S_1=B_{12}-B_{22}\\ S_2=A_{11}+A_{12}\\ S_3=A_{21}+A_{22}\\ S_4=B_{21}-B_{11}\\ S_5=A_{11}+A_{22}\\ S_6=B_{11}+B_{22}\\ S_7=A_{12}-A_{22}\\ S_8=B_{21}+B_{22}\\ S_9=A_{11}-A_{21}\\ S_{10}=B_{11}+B_{12}\\ \)
      3. 遞迴的計算 7 個矩陣積 \(P_1,P_2,…,P_7\)，其中每個矩陣\(P_i\)都是\(\frac{n}{2}\cdot\frac{n}{2}\)的。
        \( P_1=A_{11}\cdot S_1=A_{11}\cdot B_{12}-A_{11}\cdot B_{22}\\ P_2=S_2\cdot B_{22}=A_{11}\cdot B_{22}+A_{12}\cdot B_{22}\\ P_3=S_3\cdot B_{11}=A_{21}\cdot B_{11}+A_{22}\cdot B_{11}\\ P_4=A_{22}\cdot S_4=A_{22}\cdot B_{21}-A_{22}\cdot B_{11}\\ P_5=S_5\cdot S_6=A_{11}\cdot B_{11}+A_{11}\cdot B_{22}+A_{22}\cdot B_{11}+A_{22}\cdot B_{22}\\ P_6=S_7\cdot S_8=A_{12}\cdot B_{21}+A_{12}\cdot B_{22}-A_{22}\cdot B_{21}-A_{22}\cdot B_{22}\\\\ P_7=S_9\cdot S_{10}=A_{11}\cdot B_{11}+A_{11}\cdot B_{12}-A_{21}\cdot B_{11}-A_{21}\cdot B_{12}\\\\\\ \)
      4. 藉由 \(P_i\) 來計算得到 矩陣 \(C\)：時間\(\Theta(n^2)\)
        \( C_{11}=P_5+P_4-P_2+P_6\\ C_{12}=P_1+P_2\\ C_{21}=P_3+P_4\\ C_{22}=P_5+P_1-P_3-P_7 \)
      • 綜合已上可得：
        • \( T(n)=\bigg\lbrace \begin{array}{ll} \Theta(1)&若n=1\\ 7T{\frac{n}{2}}+\Theta(n^2)&若n>1 \end{array} \)
        • 故時間複雜度可推得 \(T(n)=\Theta(n^{\log_27})\approx \Theta(n^{2.807})\)
      • 參考來源 Wikipedia

3. 合併排序 Merge Sort

  • 在[Algo] 0-4. 二元樹(Binary Tree)中有介紹過，合併排序跟快速排序都有著類似前序、後序的結構，
  • 步驟：
    1. 將數列拆成若干個只有 1 個元素的子數列(因為只有一個元素，所有可以視為已排序的數列)。
    2. 將已排序的數列兩兩合併，直到所有的數列都合併完成，即完成排序。
  • 程式碼實作：mergeSort

4. 快速排序 Quick Sort

  • 步驟：
    1. 選定一個數當作樞紐(pivot)，將小於此數的值都放到左邊，大於此數的都放到右邊。
    2. 反覆同樣動作，直到子數列只有一個數，即完成排序。
  • 程式碼實作：quickSort

三、例題

1. 樹類問題

  • 樹相關的問題很常有著類似的解題結構：

    • 在 base state 時，直接回傳答案(base result)。
    • 對根的節點做遞迴的處理
    • 將遞迴過後的回傳值做處理之後回傳。
    T function(TreeNode* root) {
    if (BASE_STATE) return BASE_RESULT;
    T left = function(root->left);
    T right = function(root->right);
    T res = SOME_OPERATION(left, right, root);
    return res;
}

    1. Maxmium Binary Tree

    • Leetcode 654. Maximum Binary Tree
    • 給定一個數列，數列中的最大值為根，其索引值比根的索引值還小的子數列形成另一個子節，比根的索引值還大的子數列同樣形成另一個子節，以此類推。 max barytree
      • 以分治法的想法思考，我們會想得到一個函式 f(nums, s, e)，s 代表數列的最小索引值，e 代表數列的最大索引值，若 r 為該數列最大值的索引值，那麼我們應該會得到一個節點，其左子節點為 f(nums, s, r-1)，右子節點為 f(nums, r+1, e。
      • 分治法的目標是要將問題由大化小，直到 base state 出現(即可以直接得到結果的一個狀態)，以此題而言就是當 s == e 或 s < e 時，
        • s == e 時，應該要回傳 new TreeNode(s)。
        • s < e 時，應該要回傳 NULL。
      • 根據上面的分析可以得到下面完整的程式碼：
      TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
    return build(nums, 0, nums.size()-1);
}
TreeNode* build(vector<int>& nums, int start, int end) {
    if (start > end) return nullptr;
    if (start == end) return new TreeNode(nums[start]);
    int r = start;
    for (int i = start; i <= end; i++) {
        if (nums[i] > nums[r]) r = i;       // 找尋最大值的索引值
    }
    TreeNode* left = build(nums, start, r-1);
    TreeNode* right = build(nums, r+1, end);
    return new TreeNode(nums[r], left, right);
}

    2.Balance a Binary Search Tree

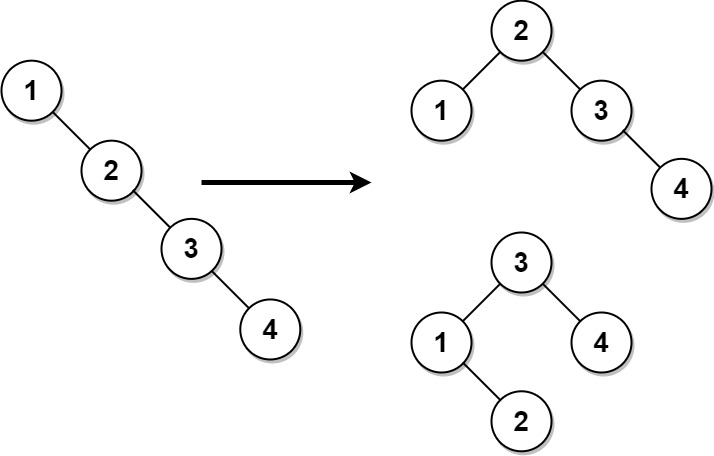
    • Leetcode 1382. Balance a Binary Search Tree balance BST
    • 這題若想要用 rotate 的方式去思考會很難解，但若把它想成是一個已排序的數列，要進行 BST 的建樹的話，就非常簡單了。
    • 首先我們想得到一個已排序的數列，我們可以用 inorder traversal(中序遍歷) 去收集所有的節點。
    • 剩下的部分就跟Leetcode 108. Convert Sorted Array to Binary Search Tree一樣了，當我們將數列索引值正中間的節點擺在根節點，那麼一定會滿足其兩邊的深度差不超過 1。
    • 用分治法的思維，我們會想得到一個函式f(vec, s, e)，s 代表數列的最小索引值，e代表數列的最大索引值，若 mid 為該數列最中間的索引值，那麼我們會得到一個節點，其左子節點為 f(vec, s, mid-1，右子節點為 f(vec, mid-1, e)。
    • 其 base state 為 s == e 或 s < e 時，
      • s == e 時，回傳 vec[s]。
      • s > e 時，回傳 NULL。
    • 根據上面的分析可得完整的程式碼：
        TreeNode* balanceBST(TreeNode* root) {
    vector<TreeNode*> vec;
    collect(root, vec);
    return build(vec, 0, vec.size()-1);
}
// 中序遍歷以收集到已排序的節點數列
void collect(TreeNode* root, vector<TreeNode*>& vec) {
    if (!root) return;
    collect(root->left,vec);
    vec.push_back(root);
    collect(root->right,vec);
    root->left = nullptr;   // 預先將節點之間的關係先清除
    root->right = nullptr;

}
TreeNode* build(vector<TreeNode*>& vec, int start, int end) {
    if (start > end) return nullptr;
    if (start == end) return vec[start];
    int mid = start + (end-start)/2;        // 求中間點
    auto left = build(vec, start, mid-1);
    auto right = build(vec, mid+1, end);
    vec[mid]->left = left;
    vec[mid]->right = right;
    return vec[mid];
}
    • 從上面兩個範例可以發現，樹類應用分治法於建樹問題上，基本上有著分常相似的框架，基本上都是想辦法把大問題拆成若干個同質的小問題，直到拆成 base state 之後再將答案組合起來。

2. Quick Select

  • Quick select 跟 quick sort 很類似，只是 quick select 選定一個 pivot 後，只針對一邊繼續做 select，假設每次都可以選到 median，則時間複雜度是 \(O(n)+O(\frac{n}{2})+O(\frac{n}{4})+…+O(\frac{n}{2^k})+O(1)=O(n)\)。但也有可能每次都剛好選到最大值或最小值，則時間複雜度會退化成\(O(n^2)\)。

    1. Kth Largest Element in an Array

    int findKthLargest(vector<int>& nums, int k) {
k = nums.size()-k;
nth_element(nums.begin(), nums.begin()+k, nums.end());
return nums[k];
}
    • 以下為彷照其核心思想的實作：
    int findKthLargest(vector<int>& nums, int k) {
    return nth(nums, nums.size()-k);
}
int nth(vector<int>& nums, int k) {
    int left = 0;
    int right = nums.size()-1;
    while (left < right) {
        int pivot = partition(nums, left, right);
        if (pivot < k) {
            left = pivot+1;
        } else if (pivot > k) {
            right = pivot-1;
        } else {
            break;
        }
    }
    return nums[k];
}
// 避免時間複雜度退化成 O(n^2) 的方法, 確保每次選到的 pivot 都是相對中間的值
void med(vector<int>& nums, int left, int right) {
    int mid = left + (right-left)/2;
    if (nums[left] >= nums[mid] && nums[mid] >= nums[right]) {
        return;
    } else if (nums[left] >= nums[mid] && nums[left] >= nums[right]) {
        if (nums[mid] >= nums[right]) {
            swap(nums[left], nums[mid]);
        } else {
            swap(nums[left], nums[right]);
        }
    } else if (nums[left] <= nums[mid] && nums[left] <= nums[right]) {
        if (nums[mid] >= nums[right]) {
            swap(nums[left], nums[right]);
        } else {
            swap(nums[left], nums[mid]);
        }
    }
}
int partition(vector<int>& nums, int left, int right) {
    med(nums, left, right);
    int pivot = left;
    int i = left;
    int j = right+1;
    while (i < j) {
        while (i < right && nums[++i] < nums[pivot]);
        while (j > left && nums[pivot] < nums[--j]);
        if (i >= j) break;
        swap(nums[i], nums[j]);
    }
    swap(nums[pivot], nums[j]);
    return j;
}
  • 二元搜索法是經典的分治法應用之一，試想一個情景，若你有一本電話簿，已知電話簿是按照 alphabetical order 排序(按字母排序)，那麼你會使用什麼樣的策略快速的找到你想要找的人的電話號碼呢？
    • 假設我們要找的人叫作 Willy。
    • 若用線性搜索法，從第一頁開始一頁一頁的找，直到找到 Willy，我們需要找完 A, B, C, ….,U, V 字首的名字才能找到 W 字首的頁面，也就是說其實 A - U 這段查找其實是多餘的，這樣的搜索法時間複雜度是 \(O(n)\)，寫成程式碼會是這樣：
    string findWilly(vector<pair<string, string>> book) {
    for (int i = 0; i < book.size(); i++) {
        if (book[i].first == "Willy") return book[i].second;
    }
    return "Not Found";
}
    • 若用二元搜索法，我們可以任意從書的中間選一頁，若選到的字首在 W 之前，我們只需從這頁開始往後，再任選一頁；反之，若選到的字首在 W 之後，我們只需從這頁開始往前，再任選一頁，重覆上面的動作直到找到 W，再依同樣的方法，找第二個字母。這樣的搜索法，時間複雜度是 \(O(\log n)\)，寫成程式碼會是這樣：
    string findWilly(vector<pair<string, string>> book) {
    int left = 0, right = book.size()-1;
    while (left <= right) {
        int mid = left + (right-left)/2;
        if (nums[mid].first == "Willy")
            return nums[mid].second;
        else if (nums[mid].first < "Willy")
            left = mid + 1;
        else if (nums[mid].first > "Willy")
            right = mid -1;
    }
    return "Not Found";
}

      + 其中 `int mid = left + (right-left)/2` 是求中間值的寫法，為什麼不寫成 `int mid = (left+right)/2` 的原因是，避免兩數相加會溢數。
    • 遇到 strictly increase 的題目，二元搜索法的基本寫法如上，是左閉右閉的寫法，另一種常見的寫法是左閉右開的寫法。
    • 當遇到非 strictly increase 的題型，就會伴隨著左限跟右限的題型出現，這部分的詳細內容會在之後二元搜索篇詳細介紹。