本文是筆者基於工作上統計製程控制(Statistical Process Control, SPC) 的心得與學習筆記，可能有紕漏，僅供參考。

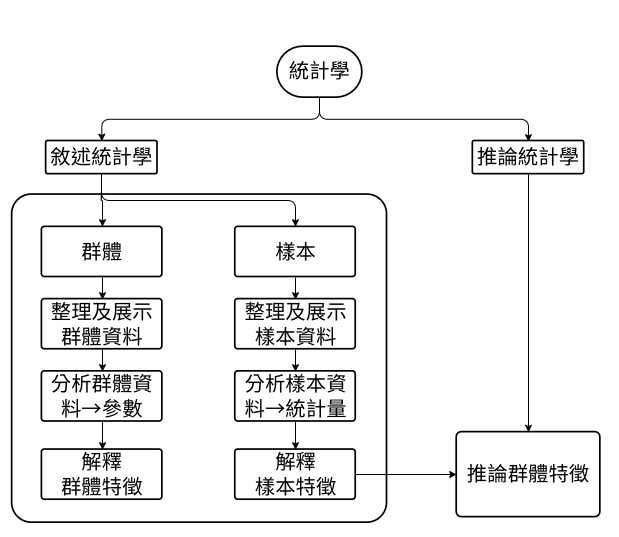
統計學(Statistics)

基本名詞

  • 群體(population)：研究對象的主體。
    • 如上例的\(\red{\text{全國人民的政治傾向}}\)、\(\red{\text{此家工廠的產品品質}}\)。
  • 樣本(sample)：群體的一部分。
    • 如上例的\(\red{\text{台灣部分的民眾}}\)、\(\red{\text{工廠部分的抽樣}}\)。
      • 目的：了解美國總統大選誰會獲勝?
      • 群體：美國有投票權的公民 此時不是美國公民的台灣民眾，就不會是這個題目的樣本。
  • 參數(parameter)：由群體資料所計算之群體表徵值。
  • 統計量(statistic)：由樣本資料所計算之樣本表徵值。

為何需要統計學?

  • 統計學是一種工具，人們為了下決策所作的一系列蒐集資料、整理、分析、與解析，是目的導向的。
    • 比方說，每次總統大選會花費大量人力，動員全國上下公教人員，花錢印選舉公報、印選票，選後還要花費大量的時間開票、驗票。假如我只是個學生想了解目前國家人民的政治傾向，不可能收集台灣上下每個人的答案，所以我們會進行抽樣。
    • 比方說工廠出貨會抽樣調查產品有沒有損壞，不可能全部的產品都拿去做測試，因為成本太高。
  • 藉由普查或抽樣的結果來描述全體的行為，作為決策的依據。
  • 統計的目的：\(\red{\text{由樣本資料推論母體參數}}\)。
    statistics

解決統計問題的五大步驟

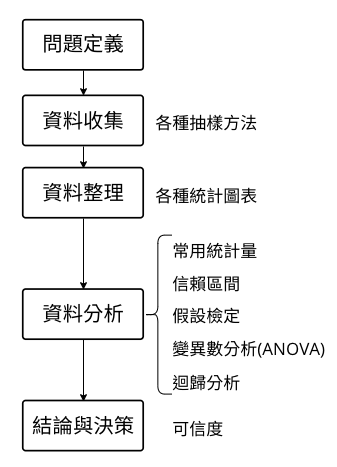
steps

問題定義

先決定你要討論的問題，跟此問題可能相關的對象為何？可以收集哪些資料？

  • 定義問題的群體與樣本。
    • 例如：我想了解 A 工廠「晶片良率」，我認為可能跟「晶片厚度」有關係。
      • 群體：A 工廠生產的晶片良率
      • 樣本：某段時間內 A 工廠某機台生產晶片的厚度
    • 例如：我想了解 B 國小附幼「小朋友學習狀況」，我認為可能跟「A 考卷的成績」有關。
      • 群體：B 國小附幼小朋友的學習狀況
      • 樣本：某次活動後的一次學習單成績。

資料收集

要收集哪些資料？哪些資料有可能可以協助我解決我想了解的問題？
例如，收集晶片的氧化層厚度、爐管的溫度、機台的編號、機台的廠商

測量尺度

  • 等比尺度(Ratio measurements)：具有零值且資料間的距離是相等被定義的。
    • 如晶片的氧化層厚度
  • 等距尺度(Interval measurements)：資料間的距離是相等被定義的，定零值並非絕對的無，而是自行定義的。
    • 如爐管的溫度(攝氏)
  • 順序尺度(Ordinal measurements)：數據的意義是並非表現在值上而是在其順序上。
    • 如機台的編號
  • 名目尺度(Nominal measurements)：測量值不具量的意義。
    • 如機台的廠商

資料整理

很多時候我們光看數字，會對研究主體沒感覺，所以引入畫圖來協助我們判斷資料。

  • 資料的整理分為兩個部分：

審查資料

  • 篩選有用的資料，收集來的資料是不是與預想的一致，資料是否有錯誤、遺漏、矛盾或是其它可疑的地方？應立刻設法檢查並更正。如果資料由不同單位蒐集而來，可能需要經過正常化(normalization)加以換算統一。太過複雜的資料應依照研究目的加以整理，以求簡化，並藉以顯示研究對象全體的通則。

資料表現

  • 資料經過整理分析得到一些統計結果，為了方便說明，我們常以圖表的方式陳示出來，以供參考使用。

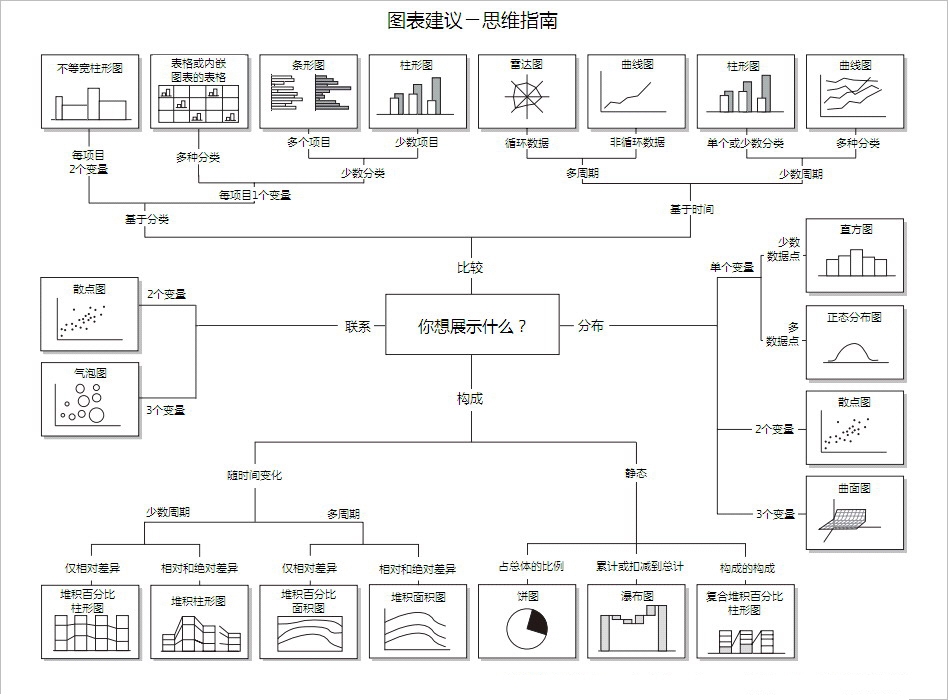
charts

  1. 散點圖(Scatter plot): 可以看相關係數 scatter

  2. 常態分布圖(高斯分布圖 normal distribution, gauss distribution)：
    可以看數據分布→變異數(低濶峰變異數大，高狹峰變異數小) guass

  3. 直方圖：跟常態分布圖用途接近，當數據點少的時候使用。

  4. 條狀圖(柱狀圖)：分類

  5. 折線圖：看時間趨勢(看股票?)

  6. 圓餅圖：看組成

  7. 瀑布圖：看累計量(也是看股票?)

  8. 累積直方圖(CDF)： CDF 族繁不及備載…

資料分析

從圖表看到的有時候過於直觀，
於是我們開始用你收集到的資料來做數學，然後進一步分析。
有比較基本、常用的「統計量」與、「指標」(如平均數、標準差)，
也有比較進階的根據不同領域所設計的「進階指標」(如吉尼係數(研究貧富差距))。

常用統計量、指標

統計量用來描述研究對象的表徵，
例如一家公司的年薪中位數，可以了解這家公司的薪資水準。
例如西瓜班的平均身高，可以了解在同齡的小朋友身高狀況。
例如新竹市市民的家庭收入標準差，可以了解新竹市的貧富差距狀況。 統計量不外乎就是用來描述「程度」與「分布」。

  • 集中趨勢：用來描述研究對象(大多數)的「程度」。
    • 平均數
      • 群體平均數：\(\boxed{\mu=\frac{\sum X_i}{N}}\)
      • 樣本平均數：\(\boxed{\bar{X}=\frac{\sum X_i}{n}}\)
    • 中位數：最中間的那個值
    • 眾數：重複最多次的那個值
  • 離中趨勢：用來描述研究對象「分佈的情形」
    • 全距：
      • \(\boxed{R=\text{Max}-\text{Min}}\)
      • 當數據有離群值時，會失去離中趨勢代表性。
    • 變異數：
      • 群體變異數：\(\boxed{\sigma^2=\frac{\sum(X_i-\mu)^2}{N}}\)
      • 樣本變異數：\(\boxed{S^2=\frac{\sum(X_i-\bar{X})^2}{n-1}}\)
        (記得樣本數的分子要減)
        • 比較好算的版本
          • \(\boxed{\sigma^2=\frac{\sum_i^NX_i^2-(\sum_i^NX_i)^2/N}{N}}\)
          • \(\boxed{S^2=\frac{\sum_i^nX_i^2-(\sum_i^nX_i)^2/n}{n-1}}\)
    • 標準差：變異數的平方，單位跟平均數一樣，在應用上可以做加減。
      • 群體標準差：\(\boxed{\sigma=\sqrt{\sigma^2}=\sqrt{\frac{\sum(X_i-\mu)^2}{N}}}\)
      • 樣本標準差：\(\boxed{S=\sqrt{S^2}=\sqrt{\frac{\sum(X_i-\bar{X})^2}{n-1}}}\)
  • 偏態：數據分佈的「形態」口訣：\(\red{\text{平地、山腰、種樹}\rightarrow\text{平均數、中位數、眾數}}\)
    • 對稱：\(\red{\text{平均數=中位數=眾數}(山頂在中間)}\)
    • 右偏、正偏：\(\red{\text{平均數>中位數>眾數}(山頂在左邊)}\)
    • 左偏、負偏：\(\red{\text{平均數<中位數<眾數}(山頂在右邊)}\) skew
    • 偏態係數 \(\text{g}_1\)
      • \(\gray{\text{g}_1=\frac{\sum_i^n(X_i-\bar{X})^3/(n-1)}{S^3}}\)
      • \(\red{\text{g}_1\text{=0表示對稱}}\)
      • \(\red{\text{g}_1\text{>0表示右偏}}\)
      • \(\red{\text{g}_1\text{<0表示左偏}}\)
  • 峰態：山頂高不高
    • 峰度係數 \(\text{g}_2\)
      • \(\gray{\text{g}_1=\frac{\sum_i^n(X_i-\bar{X})^4/(n-1)}{S^4}-3}\)
      • \(\red{\text{g}_2\text{=0表示常態分佈}}\)
      • \(\red{\text{g}_2\text{>0表示高狹峰}}\)
      • \(\red{\text{g}_2\text{<0表示低濶峰}}\) kurtosis

正態分布解析

  • 若一組資料滿足自然分布(高斯分布、常態分布、正態分布、鐘型分布)，便會滿足以下的性質。
    • 68、95、99.7 原則
      1. 即平均值一倍標準差內佔 68.27%。
      2. 即平均值二倍標準差內佔 95.45%。
      3. 即平均值三倍標準差內佔 99.73%。
      • 不受高狹峰或低濶峰影響。
      • 但偏態則會影響。
      • 百分位數、百分等級、z 分數、t 分數都可以是從這個固定的分配比例衍生來的。
    • 百分位數(Ppr、Pp)
      • 代表「累計百分比」
      • 小明某次考試 90 分贏過 70% 的考生，小明的百分位數即為 70。
    • 百分等級
      • 與「資料的個數」有關
      • \(\text{PR=}100\times R+\frac{50}{N}\)
      • 小明在 10 個人中排第 3 名，表示他贏過 7 個人，累計百分比為 70%， \(\text{PR=}100\times 70\%+\frac{50}{\red{10}}=70+5=75\)
      • 小明如果考 90 分，則此次考試 PR 75 的原始分數即為 90 分。
      • 小明如果在 50 個人中排第 15 名，同樣的累計百分比為 70 %，但是 PR 值變成 \(\text{PR=}100\times 70\%+\frac{50}{\red{50}}=70+1=71\)
      • 小明如果是參加五萬人的選拔，同樣贏過 70% 的人，
        \(\text{PR=}100\times 70\%+\frac{50}{\red{50000}}=70+0.001=70.001\approx70\\ \red{\text{PR只分100個等級，故不會有小數點，所以要四捨五入，}\\\text{換言之，受試者超過101人，PR=Ppr}}\)
    • 累積百分比與標準差
      • \(-3\times\sigma=50\%-99.73\%/2\approx0.1\%\)
      • \(-2\times\sigma=50\%-95.45\%/2\approx2.3\%\)
      • \(-1\times\sigma=50\%-68.27\%/2\approx15.9\%\)
      • \(+0\times\sigma=50\%\)
      • \(+1\times\sigma=50\%-68.27\%/2\approx84.1\%\)
      • \(+2\times\sigma=50\%-95.45\%/2\approx97.7\%\)
      • \(+3\times\sigma=50\%-99.73\%/2\approx99.9\%\)
    • z 分數
      • 換言之就是標準差。
      • 小明贏過 84.1% 的人，z 分數即為 +1。
      • 小明贏過 2.3% 的人，z 分數即為 -2。
    • t 分數
      • 設定百分位數 50% 為 50 分，每增加一個標準差多 10分 反之亦然。
      • 公式：\(\boxed{z = \frac{t-50}{10}}\) 或 \(\boxed{t=10z+50}\)
      • 小明的 t 分數是 70 分，代表它的 z 分數是 +2，累計百分比是 97.7%，百分位數是97.7，假設受試人超過101人，PR等級為 98。 gauss

信賴區間

用以一段區間描述研究對象。
例如，95% 信賴水準下，台灣男生的身高為 160~180 公分。代表你去路上隨機街訪，大約95% 的機率，路人(男)的身高都會落在 160~180 公分以內。
注意以上的描述不一定為真，因為抽樣結果與群體間會有誤差。

  • 假設我今天做了一個台灣男生身高抽樣調查，結果結果剛好呈現常態分布，並且平均身高是 170 公分，標準差是 5 公分。
    • 68% 信賴水準下，台灣的男生身高會落在 165~175 公分的區間內。
    • 95% 信賴水準下，台灣的男生身高會落在 160~180 公分的區間內。
    • 99.7% 信賴水準下，台灣的男生身高會落在 155~185 公分的區間內。
  • 信賴水準 \(1-\alpha\)：從上例可見，當信賴區間增加，信賴水準也會增加。
  • 顯著水準 \(\alpha\)：反之，顯著水準增增加，代表愈寬鬆。通常定為 0.05。
    • 白話：你只有 5% 的機率找到例外。
    • 假設今天收集的數據不為常態分布，為左偏或右偏，它可以滿足 99.7% 的信賴區間，但不一定滿足 95% 信賴區間。
  • P 值：
    • 定義：假使虛無假設是真的，實際觀測獲得比取樣更極端的值的機率是多少。
    • 白話：假設台灣男生的身高都落在 160~180 公分之間，找到比 160 公分以下和 180 公分以上的機率是多少？
      • P 值無法用來證明何者絕對正確，只能透過機率來「合理推斷」
    • 跟\(\alpha\)的關係：
      • 假設我做了一次調查，發現 1000 個人之中只有 20 個人高於 180 公分或矮於 160 公分，即 P 值為 0.02。
      • 此時若此份調查宣稱信賴水準是 95%，即 \(\alpha=0.05\)，則我們可以推斷這份調查是準確的，所以我們無法拒絕虛無假設。
      • 此時若此份調查宣稱信賴水準是 99%，即 \(\alpha=0.01\)，則我們可以推斷這份調查可能不準確，所以我們可以拒絕虛無假設。
        • 也就是如果調查是正確的，我們應該只能從 1000 個人裡面找到小於 10 個極端值。不過因為 P 值是機率，我們可以拒絕，但不表示調查就是完全不正確的，也許我們再擴大調查，也許有可能在 10000 個人裡面總共只找到 45 個極端值，那這份調查又變成有效的了。

假設檢定

test

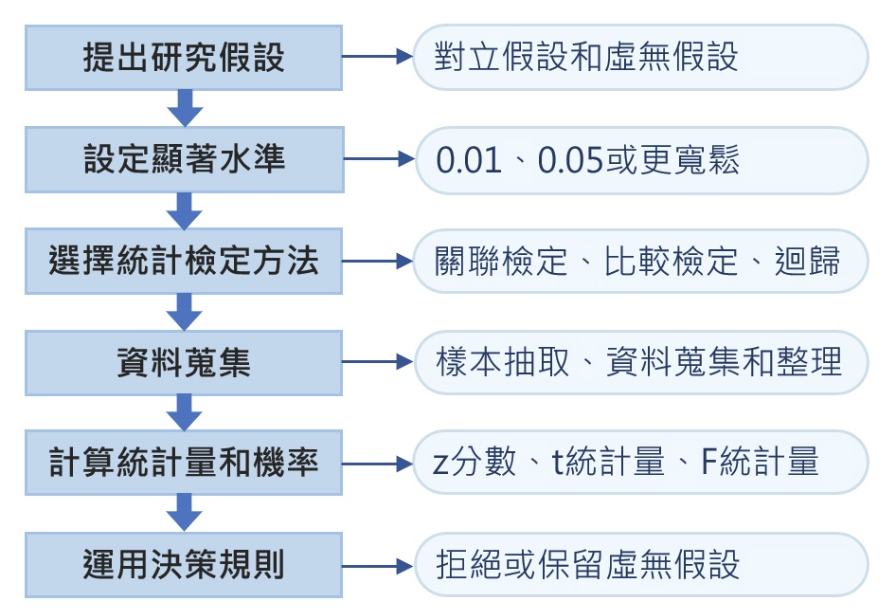
  • 單尾、雙尾
    • 單尾代表只有一個拒絕域，右分為左尾與右尾。
      • 左尾：台灣男性有 95% 都高於 160 公分。
      • 右尾：台灣男性有 95% 都矮於 180 公分。
    • 雙尾代表有兩個拒絕域
      • 雙尾：台灣男生有 95% 落在 160 公分到 180 公分的區間內。

結論與決策

可信度

當你做完數據，你的最終目的是想把你的研究對象跟你的調查數據關聯起來，這個關聯性必須要有可信度。
前面的一大堆資料分析、檢定目的在於「證明抽樣有沒有辦法代表母體」。 現在「兩個足以代表母體的數據」，就可以來測試關聯性。

  • 相關係數
    • 以下的圖稱為散佈圖，把兩個數據分別放於 X 軸與 Y 軸，如果兩者是相關的，表示在座標平面上，你可以找到「一條線(趨勢線)」(不一定要是直線)來描述他。
    • 為什麼不一定要是直線? 因為 X軸跟 Y 可以是不同的尺規，X-Y 也有可能是對數尺規或是指數尺規。
    • |相關係數|愈高，則數據愈貼近趨勢線。 一般來說，
      • \(\gamma=1\)，完全線性正相關。
      • \(\gamma=-1\)，完全線性負相關。
      • \(0.7\le\gamma<1\)，強正相關。
      • \(-0.7\ge\gamma>-1\)，強負相關。
      • \(0.3\le\gamma<0.7\)，弱正相關。
      • \(-0.3\ge\gamma<-0.7\)，弱負相關。
      • \(-0.3<\gamma<0.3\)，無相關。
    • 工程上喜歡用 \(R^2\) 來表示相關性，其實就是相關係數的平方，不討論正、負相關，只考慮相關性。

corr

最後的最後

  • 你學會了定義問題、收集資料、整理資料、資料分析跟最後的關聯性分析，你就可以下結論並做決策了！是不是很棒啊。
    • 記得統計學只是工具，過程一定要有問題，目標是下決策。
    • 例如，我想知道怎麼樣提升學生的學習成效。
      我發現學生的學習成效跟讀書時間的長短呈現強相關，且讀書時間愈長，學習成效愈好。那麼作為一名老師，我還不叫你把書讀爆！就是在說你，還不快點去讀書！！