1339. Maximum Product of Splitted Binary Tree
- Hardness: \(\color{orange}\textsf{Medium}\)
- Ralated Topics:
Tree、Depth-First Search、Binary Tree
一、題目
Given the root of a binary tree, split the bianry tree into two subtrees by removing one edge such that the product of the sums of the subtreesis maximized.
Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 10^9 + 7.
Note that you need to maximize the answer before taking the mod and not after taking it.
Example 1: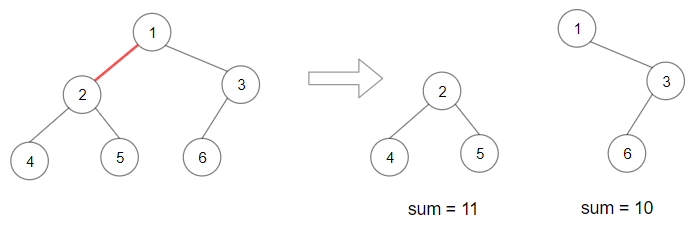
- Input: root = [1,2,3,4,5,6]
- Output: 110
- Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (10*10)
Example 2:
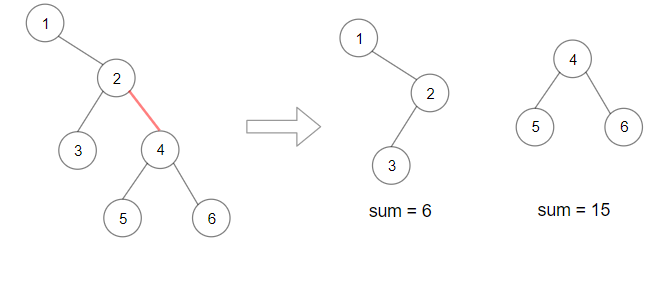
- Input: root = [1,null,2,3,4,null,null,5,6]
- Output: 90
- Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Constraints:
- The number of nodes in the tree is in the range
[2, 5 * 10^4]. 1 <= Node.val <= 10^4
二、分析
- 這一題的關鍵在於,求切斷的
edge兩邊的乘積為最大值。而一但我們知道整棵樹的總和之後,我們便只要知道切斷的其中一邊的和為多少,便可以知道另一邊的和為多少。one = total - another
- 經觀察我們可以發現,節點與其所有子葉的和,代表了切斷的
edge的其中一邊。 - 故我們只需遍歷整個樹,並把當下節點與所有子葉的和,記錄到
vector中,再利用one = total - another的關係,求得最大乘積。 - 需要注意此題為大數問題,要注意返回的值要先比較之後才取餘數。
三、解題
1. DFS
- Time complexity: \(O(n)\)
- Space complexity: \(O(n)\)
#define ll long long int
#define MOD 1000000007
int maxProduct(TreeNode* root) {
vector<ll> vec;
int total = dfs(root, vec); // 遍歷樹,並算出整棵樹的和
ll res = 0;
for (ll& x : vec) {
res = max(res, x * (total-x)); // 截斷邊的兩側樹的和分別為 x 與 total - x
}
return res % MOD;
}
int dfs(TreeNode* root, vector<ll> vec) {
if (!root) return 0;
int left = dfs(root->left, vec);
int right = dfs(root->right, vec);
vec.push_back(root->val + left + right); // 將子樹的總和記到 vector 中
return vec.back(); // 返回子樹的總和,讓父節點可以使用
}