1706. Where Will the Ball Fall

  • Hardness: \(\color{orange}\textsf{Medium}\)
  • Ralated Topics: Array、Dynamic Programming、Depth-First Search、Matrix、Simulation

一、題目

You have a 2-D grid of size m x n representing a box, and you have n balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.

  • A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as 1.
  • A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as -1.
    We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball get stuck if it hits a “V” shaped pattern between two boards or if a board redirects the ball into either wall of the box.
    Return an array answer of size n where answer[i] is the column that the ball falls out of at the bottom after dropping the ball from the ith column at the top, or -1 if the ball gets stuck in the box.

Example 1: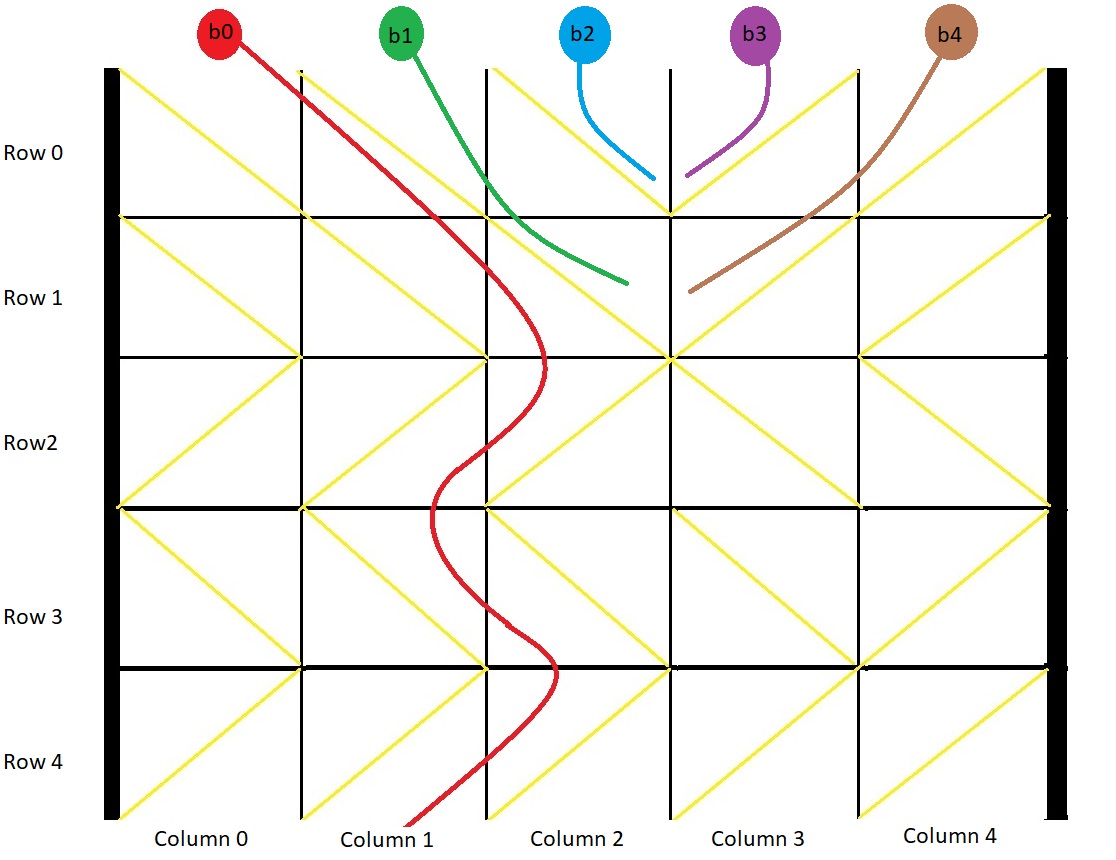
ball

  • Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
  • Output: [1,-1,-1,-1,-1]
  • Explanation: This example is shown in the photo.
    Ball b0 is dropped at column 0 and falls out of the box at column 1.
    Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
    Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
    Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
    Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.

Example 2:

  • Input: grid = [[-1]]
  • Output: [-1]
  • Explanation: The ball gets stuck against the left wall.

Example 3:

  • Input: grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]
  • Output: [0,1,2,3,4,-1]

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100
  • grid[i][j] is 1 or -1.

二、分析

  • 這一題根據題意，球在落下的過程中，若碰到v-型或是牆，都會被卡住，可以歸納出下面幾條規則：(假設以 col 代表球的位置)
    • grid[row][0] == -1 與 grid[row][n-1] == 1 代表撞到牆
    • 當 grid[row][col] == 1 且 grid[row][col+1] == 1 時球可以落下。
      或 grid[row][col] == -1 且 grid[row][col-1] == -1 時球可以落下。

三、解題

1. DP

  • Time complexity: \(O(m\times n)\)
  • Space complexity: \(O(n)\)
vector<int> findBall(vector<vector<int>>& grid) {
    int m = grid.size(), n = grid[0].size();
    vector<int> state;
    for (int col = 0; col < grid[0].size(); col++) state.push_back(col);   // 初始化球當前的位置
    for (auto& boards : grid) {
        for (int col = 0; col < n; col++) {
            if (state[col] == -1) continue;     // 球已經卡住了
            int& pos = state[col];
            if ((pos == 0 && boards[pos] == -1) || (pos == n-1 && boards[pos] == 1))    // 撞牆
                pos = -1;
            else if (boards[pos] == 1 && boards[pos+1] == 1)        // 球往右移
                pos += 1;
            else if (boards[pos] == -1 && boards[pos-1] == -1)      // 球往左移
                pos -= 1;
            else                                                    // 球卡住
                pos = -1;
        }
    }
    return state;
}

2. DFS

  • Time complexity: \(O(m\times n)\)
  • Space complexity: \(O(n)\)
int m, n;
vector<int> findBall(vector<vector<int>>& grid) {
    m = grid.size(), n = grid[0].size();
    vector<int> res(n);
    for (int col = 0; col < n; col++) {
        res[col] = dfs(grid, 0, col);
    }
    return res;
}
int dfs(vector<vector<int>>& grid, int row, int col) {
    if (row == m) return col;           // 終止條件: 落地
    if (col < 0 || col >= n) return -1; // 撞牆
    if (col+1 < n && grid[row][col] == 1 && grid[row][col+1] == 1)  // 右移
        return dfs(grid, row+1, col+1);
    if (col-1 >= 0 && grid[row][col] == -1 && grid[row][col-1] == -1)   // 左移
        return dfs(grid, row+1, col-1);
    return -1;   
}

回目錄 Catalog