2463. Minimum Total Distance Traveled

  • Hardness: \(\color{red}\textsf{Hard}\)
  • Ralated Topics: Array、Dynamic Programming、Sorting
  • \(\color{blue}\textsf{Weekly Contest 318}\)

一、題目

There are some robots and factories on the X-axis. You are given an integer array robot where robot[i] is the position of the ith robot. You are also given a 2D integer array factory where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.

The positions of each robot are unique. The positions of each factory are also unique. Note that a robot can be in the same position as a factory initially.

All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.

At any moment, you can set the initial direction of moving for some robot. Your target is to minimize the total distance traveled by all the robots.
Return the minimum total distance traveled by all the robots. The test cases are generated such that all the robots can be repaired.

Note that

  • All robots move at the same speed.
  • If two robots move in the same direction, they will never collide.
  • If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
  • If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
  • If the robot moved from a position x to a position y, the distance it moved is |y - x|.

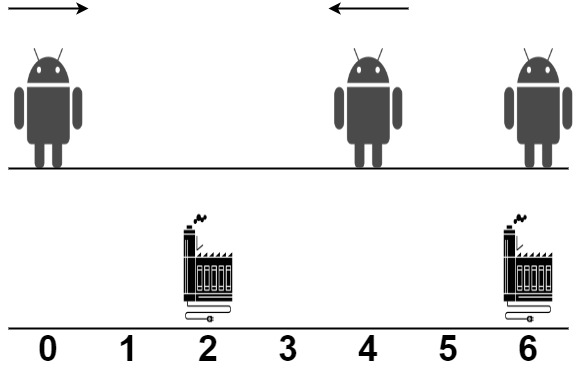ex1 Example 1:

  • Input: robot = [0,4,6], factory = [[2,2],[6,2]]
  • Output: 4
  • Explanation: As shown in the figure:
  • The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
  • The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
  • The third robot at position 6 will be repaired at the second factory. It does not need to move.
    The limit of the first factory is 2, and it fixed 2 robots.
    The limit of the second factory is 2, and it fixed 1 robot.
    The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.

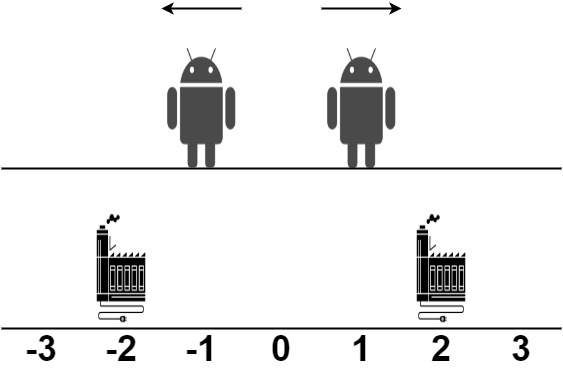ex2 Example 2:

  • Input: robot = [1,-1], factory = [[-2,1],[2,1]]
  • Output: 2
  • Explanation: As shown in the figure:
  • The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
  • The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.
    The limit of the first factory is 1, and it fixed 1 robot.
    The limit of the second factory is 1, and it fixed 1 robot.
    The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.

Constraints:

  • 1 <= robot.length, factory.length <= 100
  • factory[j].length == 2
  • -10^9 <= robot[i], positionj <= 10^9
  • 0 <= limitj <= robot.length
  • The input will be generated such that it is always possible to repair every robot.

二、分析

  • 初見此題，最先想到的方法是 Greedy + Binary Search，想法是每個機器人都先找離自己最近的工廠，解法參考如下，但實際上，第一個機器人的選擇會影響接下來的機器人的最近選擇：如 robot = [9,11,99,101], factory = [[7,1],[10,1],[14,1],[96,1][100,1],[103,1]]，若第一個位置在 9 的機器人選擇了位置在 10 的工廠，則會影響位置在 11 的機器人最近的工廠在 14，而這樣的選擇就導致錯過了最近解。所以這種解法還需要一些修正。
long long minimumTotalDistance(vector<int>& robot, vector<vector<int>>& factory) {
    map<int,int> mp;
    long long res = 0;
    for (auto f : factory) {
        if (f[1] == 0) continue;
        mp[f[0]] = f[1];
    }
    for (auto r : robot) {
        auto it = mp.lower_bound(r);
        if (it == mp.end()) {
            it--;
        } else if (it != mp.begin()){
            auto right = it--;
            if (r - it->first > right->first - r) {
                it = right;
            }
        }

        res += abs(it->first - r);
        if (it->second == 1) {
            mp.erase(it);
        } else {
            it->second--;
        }
    }
  • 也許可以將透過 sorting 將機器人分為幾個子群對應幾個工廠。
  • 如果用 dfs + memoization 也就是 dynamic programming 的方式應該可解，透過將 factory 扁平化，並經過 sort 的之後，令 dp(i, j) 為總步數，i 為由左數到右第 ith 個機器人，j 為由左數到右第 jth 個工廠的「空位」。

三、解題

1. DP

  • Time complexity: \(O(m\times n\times k)\)
  • Space complexity: \(O(m\times n\times k)\)
  • m = robot.size(), n = factory.size(), k = max(factory[i].size())
vector<vector<long long>> dp;
long long minimumTotalDistance(vector<int>& robot, vector<vector<int>>& factory) {
    long long res = 0;
    vector<int> fac;
    for (auto f : factory) {        // 將 factory 扁平化成 1d array
        int times = f[1];
        while (times--) {
            fac.push_back(f[0]);
        }
    }
    dp = vector<vector<long long>>(robot.size()+1, vector<long long>(fac.size()+1, -1));
    sort(robot.begin(), robot.end());
    sort(fac.begin(), fac.end());
    return dfs(robot, fac, 0, 0);
}
long long dfs(vector<int>& robot, vector<int>& fac, int i, int j) {
    if (i == robot.size()) return 0;    // 當機器人都排列完畢，為終止條件
    if (j == fac.size()) return (long long) (LONG_MAX/2);  // 工廠空缺空用了，傳回一個有效的大數，使之不會是答案
    if (dp[i][j] != -1) return dp[i][j];
    dp[i][j] = min(
        dfs(robot, fac, i+1, j+1) + (long long)abs(robot[i]-fac[j]),    // ith 機器人選擇 jth 工廠空位
        dfs(robot, fac, i, j+1)                                         // ith 機器人不選擇 jth 工廠空位
    );
    return dp[i][j];
}

回目錄 Catalog