587. Erect the Rence

  • Hardness: \(\color{red}\textsf{Hard}\)
  • Ralated Topics: Array、Math、Geometry

一、題目

You are given an array trees where trees[i] = [xi, yi] represents the location of a tree in the garden. You are asked to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed. Return the coordinates of trees that are exactly located on the fence perimeter.

Example 1:

  • Input: points = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
  • Output: [[1,1],[2,0],[3,3],[2,4],[4,2]]

Example 2:

  • Input: [[1,2],[2,2],[4,2]]
  • Output: [[4,2],[2,2],[1,2]]

Constraints:

  • 1 <= points.length <= 3000
  • points[i].length == 2
  • 0 <= xi, yi <= 100
  • All the given points are unique.

二、分析

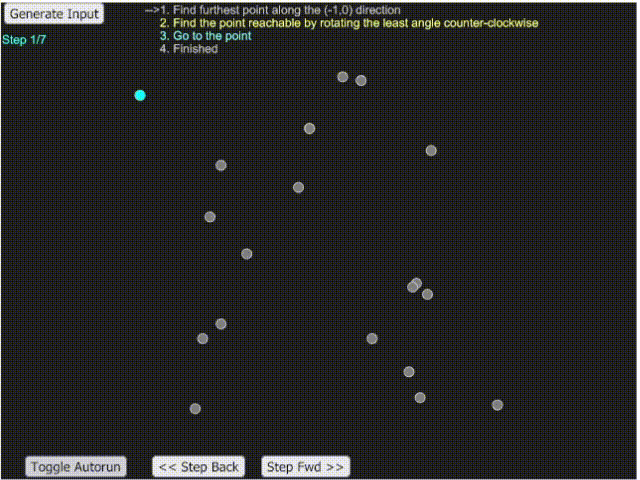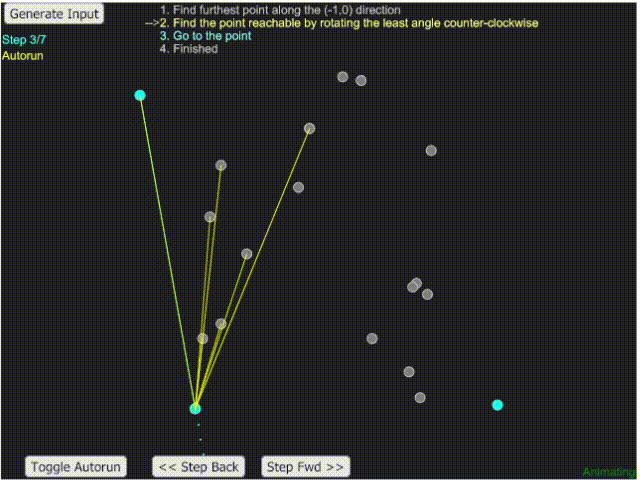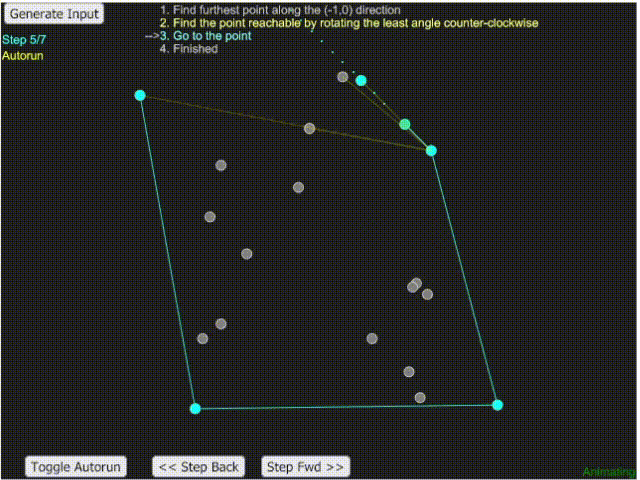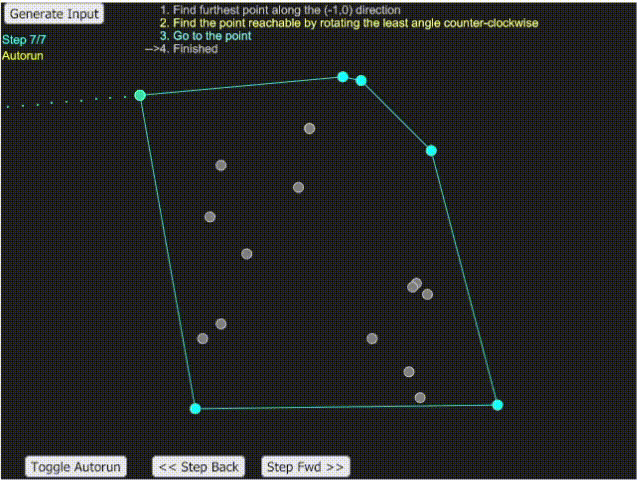
illustration

  • 這題的關鍵在於當一個點已經是最外圍的點時，其相鄰的 fence 會是與之斜率最大與最小的兩點。
  • 可將數組排序後利於解題。
  • 由左到右找斜率大的，可得到上半部的外圍線；由右到左可得到下半部的外圍線。

三、解題

1. Math

  • Time complexity: \(O(n)\)
  • Space complexity: \(O(n)\)
bool biggerSlope(vector<int>& a, vector<int>& b, vector<int>& c) {
    // slope of ab compares with slope of ac
    return (b[1]-a[1])*(c[0]-a[0]) < (b[0]-a[0])*(c[1]-a[1]);
}
vector<vector<int>> outerTrees(vector<vector<int>>& trees) {
    int n = trees.size();
    vector<vector<int>> res;
    sort(trees.begin(), trees.end());

    for (int i = 0; i < n; i++) {
        while (res.size() > 1 && biggerSlope(res[res.size()-2], res.back(), trees[i]))
            res.pop_back();
        res.push_back(trees[i]);
    }
    if (res.size() == n) return res;

    for (int i = n-2; i >= 0; i--) {
        while (res.size() > 1 && biggerSlope(res[res.size()-2], res.back(), trees[i]))
            res.pop_back();
        res.push_back(trees[i]);           
    }
    res.pop_back();
    return res;
}

回目錄 Catalog