766. Toeplitz Matrix
- Hardness: \(\color{green}\textsf{Easy}\)
- Ralated Topics:
Array、Matrix
一、題目
Given an m x n matrix, return true if the matrix is Toeplitz. Otherwise, return false. A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same elements.
Example 1: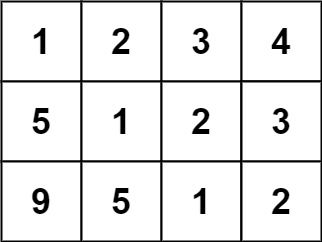
- Input: matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
- Output: true
- Explanation:
In the above grid, the diagonals are:
“[9]”, “[5, 5]”, “[1, 1, 1]”, “[2, 2, 2]”, “[3, 3]”, “[4]”.
In each diagonal all elements are the same, so the answer is True.
Example 2:
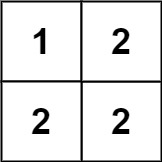
- Input: matrix = [[1,2],[2,2]]
- Output: false
- Explanation:
The diagonal “[1, 2]” has different elements.
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200 <= matrix[i][j] <= 99
Follow up:
- What if the
matrixis store on disk, and the memory is limited such that you can only load at most one row of the matrix into memory at once? - What if the
matrixis so large that you can only load up a partial row into memory at once?
二、分析
- 根據題意,除了第一行與第一列外,逐個去檢查與左上角的值是否相同。
三、解題
1. Simple traversal
- Time complexity: \(O(m\times n)\)
- Space complexity: \(O(1)\)
bool isToeplitzMatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] != matrix[i-1][j-1]) return false;
}
}
return true;
}
2. Follow up #1: load at most one row
- Time complexity: \(O(m\times n)\)
- Space complexity: \(O(n)\)
bool isToeplitzMatrix(vector<vector<int>>& matrix) {
deque<int> buffer;
for (int j = 0; j < matrix[0].size()-1; j++) buffer.push_back(matrix[0][j]); // 一次處理一行
for (int i = 1; i < matrix.size(); i++) {
for (int j = 1; j < matrix[0].size(); j++) {
if (buffer.front() != matrix[i][j]) return false;
buffer.pop_front();
buffer.push_back(matrix[i][j]);
}
buffer.push_front(matrix[i][0]);
buffer.pop_back();
}
return true;
}
3. Follow up #2: load partial row/column each time
bool isToeplitzMatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
queue<pair<int,int>> q;
for (int i = m-1; i > 0; i--) q.push({i, 0});
for (int i = 0 ; i < n; i++) q.push({0, i});
while (!q.empty()) {
auto info = q.front();
q.pop();
int row = info.first;
int col = info.second;
int val = matrix[row][col];
while (++row < m && ++col < n) {
if (matrix[row][col] != val) return false;
}
}
return true;
}