[Leetcode] 835. Image Overlap

835. Image Overlap

Hardness: \(\color{orange}\textsf{Medium}\)
Ralated Topics: Array、Matrix

一、題目

You are given two images, img1 and img2, represented as binary, square matrices of size n x n. A binary matrix has only 0s and 1s as values.
We translate one image however we choose by sliding all the 1 bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the overlap by counting the number of positions that have a 1 in both images. Note also that a translation does not include any kind of rotation. Any 1 bits that are translated outside of the matrix bordered are erased.
Return the largest possible overlap.

Example 1: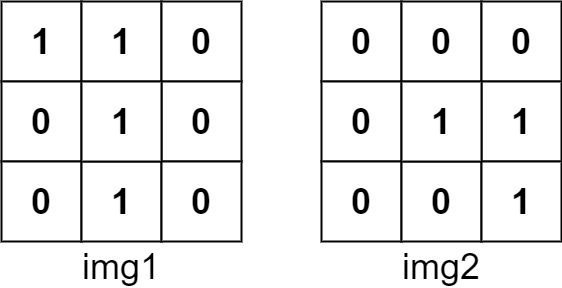
overlap1

Input: img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]]
Output: 3
Explanation: We translate img1 to right by 1 unit and down by 1 unit.
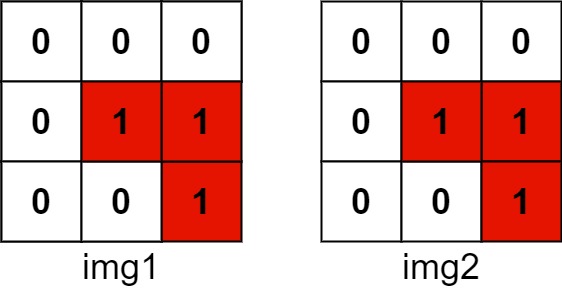
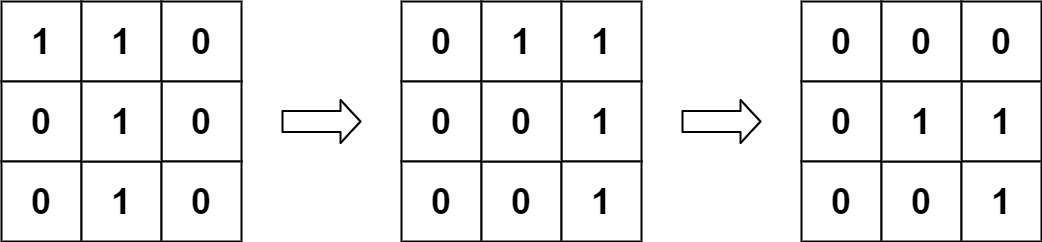The number of positions that have a 1 in both images is 3 (shown in red).

Example 2:

Input: img1 = [[1]], img2 = [[1]]
Output: 1

Example 3:

Input: img1 = [[0]], img2 = [[0]]
Output: 0

Constraints:

n == img1.length == img1[i].length
n == img2.length == img2[i].length
n <= n <= 30
img1[i][j] is either 0 or 1.
img2[i][j] is either 0 or 1.

二、分析

注意到 n 的範圍是 1 <= n <= 30。

我們可以用 bit manipulation 的方式來處理這一題。

將 vector 轉為二進制數字(n < 31)：
- 如 {1,0,0,1,0,1} 轉換成 100101。

int masking(vector<int> vec) {
    int res = 0;
    for (int i = 0; i < n; i++) {
        if (vec[i]) res |= (1 << (n-1-i));
    }
}

數二進制數字中有幾個 bit 為 1：

int count(int bit) {
    int cnt = 0;
    while (bit) {
        bit -= (bit & -bit);
        cnt++;
    }
    return cnt;
}

把 matrix 視為 n 列以二進位表示的數字。
故題目可以簡化成「求 bitset1 & bitset2 中的最大值」。
實作 upshift、downshift、leftshift、rightshift。
- upshift、downshift 我們可以看作兩張 img 的 rows 相對移動，將移動後的 row 補 0
- leftshift、rightshift 可以很簡單的靠 >> 運算子達成，但要注意用 << 可能會超出範圍，但我們可以利用 img2 向左移將相當於 img1 向右移的性質來達成。

三、解題

1. Bit Manipulation

Time complexity: \(O(n^3)\)
Space complexity: \(O(n)\)

// 計算 bit 為 1 的數目：O(1)
int count(int bit) {
    int cnt = 0;
    while (bit) {
        bit -= (bit & -bit);
        cnt++;
    }
    return cnt;
}
// 將 matrix 轉為 2 進制數字的 array：O(n^2)
vector<int> masking(vector<vector<int>>& img) {
    vector<int> res(img.size(), 0);
    for (int i = 0; i < img.size(); i++) {
        for (int j = 0; j < img[i].size(); j++) {
            if (img[i][j]) res[i] |= (1 << j);
        }
    }
    
    return res;
}
int largestOverlap(vector<vector<int>>& img1, vector<vector<int>>& img2) {
    int n = img1.size();
    if (n == 0) return 0;
    vector<int> mask1 = masking(img1);
    vector<int> mask2 = masking(img2);
    int res = 0;
    for (int v = -n+1; v < n; v++) {
        for (int h = 0; h < n; h++) {
            int cnt1 = 0;
            int cnt2 = 0;
            for (int i = 0; i < n; i++) {
                int bit1 = (i+v<0 || i+v>=n) ? 0 : mask1[i+v];   // bit 上下移，越界補 0
                int bit2 = mask2[i];
                cnt1 += count((bit1 >> h) & bit2);      // bit1 右移
                cnt2 += count((bit2 >> h) & bit1);      // bit2 右移(視為 bit1 左移)
            }
            res = max({res, cnt1, cnt2});
        }
    }
    return res;
}

回目錄 Catalog

一、題目#

二、分析#

三、解題#

1. Bit Manipulation#

一、題目

二、分析

三、解題

1. Bit Manipulation