931. Minimum Falling Path Sum

  • Hardness: \(\color{orange}\textsf{Medium}\)
  • Ralated Topics: Array、Dynamic Programming、Matrix

一、題目

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

Example 1: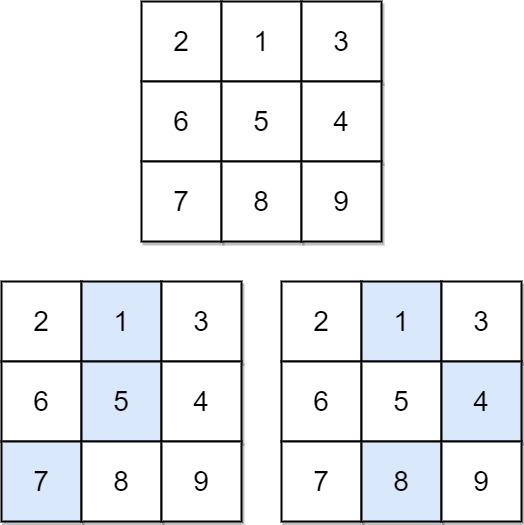
falling1-grid

  • Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]
  • Output: 13
  • Explanation: There are two falling paths with a minimum sum as shown.

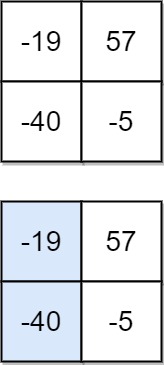falling2-grid Example 2:

  • Input: matrix = [[-19,57],[-40,-5]]
  • Output: -59
  • Explanation: The falling path with a minimum sum is shown.

Constraints:

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 100
  • -100 <= matrix[i][j] <= 100

二、分析

  • 這題也是典型的動態規劃問題，每一層可能的最小值，會影響到下一層的最小值，所以我們只需記錄每一層的狀態再將狀態往下一層推移即可。
  • 定義 dp[m][n] 為第 m 層，第 n 欄的累計最小值。
  • 轉移方程式為 dp[m][n] = min({dp[m-1][n-1], dp[m-1][n], dp[m-1][n+1]}) + row[m][n]。
    • 但要注意最左邊跟最右邊要另外處理以避免出界。
  • 從轉移方程式可以注意到，狀態的轉移只跟上一層有關係，故可以做空間壓縮，就空間複雜度壓到 \(O(n)\)

三、解題

1. DP

  • Time complexity: \(O(m\times n)\)
  • Space complexity: \(O(m\times n)\)
int minFallingPathSum(vector<vector<int>>& matrix) {
    int m = matrix.size(), n = matrix[0].size();
    if (m == 1) return matrix[0][0];
    vector<vector<int>> dp(m+1, vector<int>(n));
    for (int i = 0; i < m; i++) {
        vector<int>& row = matrix[i];
        dp[i+1][0] = min(dp[i][0], dp[i][1]) + row[0];
        dp[i+1][n-1] = min(dp[i][n-1], dp[i][n-2]) + row[n-1];
        for (int j = 1; j < n-1; j++) {
            dp[i+1][j] = min({dp[i][j-1], dp[i][j], dp[i][j+1]}) + row[j];
        }
    }
    int res = INT_MAX;
    for (int j = 0; j < n; j++) {
        res = min(res, dp[m][j]);
    }
    return res;
}

2. DP space-optimized

  • Time complexity: \(O(m\times n)\)
  • Space complexity: \(O(n)\)
int minFallingPathSum(vector<vector<int>>& matrix) {
    int m = matrix.size(), n = matrix[0].size();
    if (m == 1) return matrix[0][0];
    // 利用奇數層跟偶數層做切換
    vector<vector<int>> dp(2, vector<int>(n));
    for (int i = 0; i < m-1; i++) {
        vector<int>& row = matrix[i];
        dp[i%2][0] = min(dp[(i+1)%2][0], dp[(i+1)%2][1]) + row[0];
        dp[i%2][n-1] = min(dp[(i+1)%2][n-1], dp[(i+1)%2][n-2]) + row[n-1];
        for (int j = 1; j < matrix[0].size()-1; j++) {
            dp[i%2][j] = min({dp[(i+1)%2][j-1], dp[(i+1)%2][j], dp[(i+1)%2][j+1]}) + row[j];
        }
    }
    int res = INT_MAX;
    dp[(m-1)%2][0] = min(dp[m%2][0], dp[m%2][1]) + matrix[m-1][0];
    dp[(m-1)%2][n-1] = min(dp[m%2][n-1], dp[m%2][n-2]) + matrix[m-1][n-1];
    res = min({res, dp[(m-1)%2][0], dp[(m-1)%2][n-1]});
    for (int j = 1; j < matrix[0].size()-1; j++) {
        dp[(m-1)%2][j] = min({dp[m%2][j-1], dp[m%2][j], dp[m%2][j+1]}) + matrix[m-1][j];
        res = min(res, dp[(m-1)%2][j]);
    }
    return res;
}

回目錄 Catalog