Version Query
- Hardness: \(\color{red}\textsf{Hard}\)
- Ralated Topics:
Binary Search、Segment Tree、Heap (Priority Queue、Hash Table
一、題目
Given an information of application(APK) about its range of versions, find its corresponding OS version. If APK versions are probable for two or more OS versions, it must be belong to the latest OS version.
The given apk_info structure is given as below.
struct apk_info {
int apk_version;
int min_version = 1;
int max_version = INT_MAX;
}
Example 1:
\(\begin{array}{|l|}\hline
\text{Input: }\\
\begin{array}{|c|c|c|}\hline
\text{apk version}&\text{min OS version}&\text{max OS version}\\\hline
\text{1}&\text{14}&\text{}\\\hline
\text{2}&\text{}&\text{8}\\\hline
\text{3}&\text{12}&\text{16}\\\hline
\end{array}\\
\text{OS version query = [18,4,14,10]}\\\\
\text{Output:}\\\text{apk version = [1,2,3,0]}(0 \text{ means not found})\\\hline
\end{array}\)
Constraints:
\(\begin{array}{|l|}\hline
\text{1. 1} \le \text{Apk version < } 10^{31}\\
\text{2. 1} \le \text{OS version < } 10^{31}\\
\text{3. 1} \le \text{Query times < } 10^{31}\\\hline
\end{array}\)
二、分析
- 重點其實就是區間求極值,所以筆者最先開始想到的是線段樹,線段樹的介紹可參考這裡:Segment Tree 線段樹
- 爾後才想到這題其實概念上很接近 Leetcode 218. The Skyline Problem
- 上這張題後就懂了,把 apk version 看成建築的高度, min OS version 與 max OS version 看成建築的 x 座標,就變成一樣的題目了,差別在於把 skyline 建成之後,再對其作 binary search。
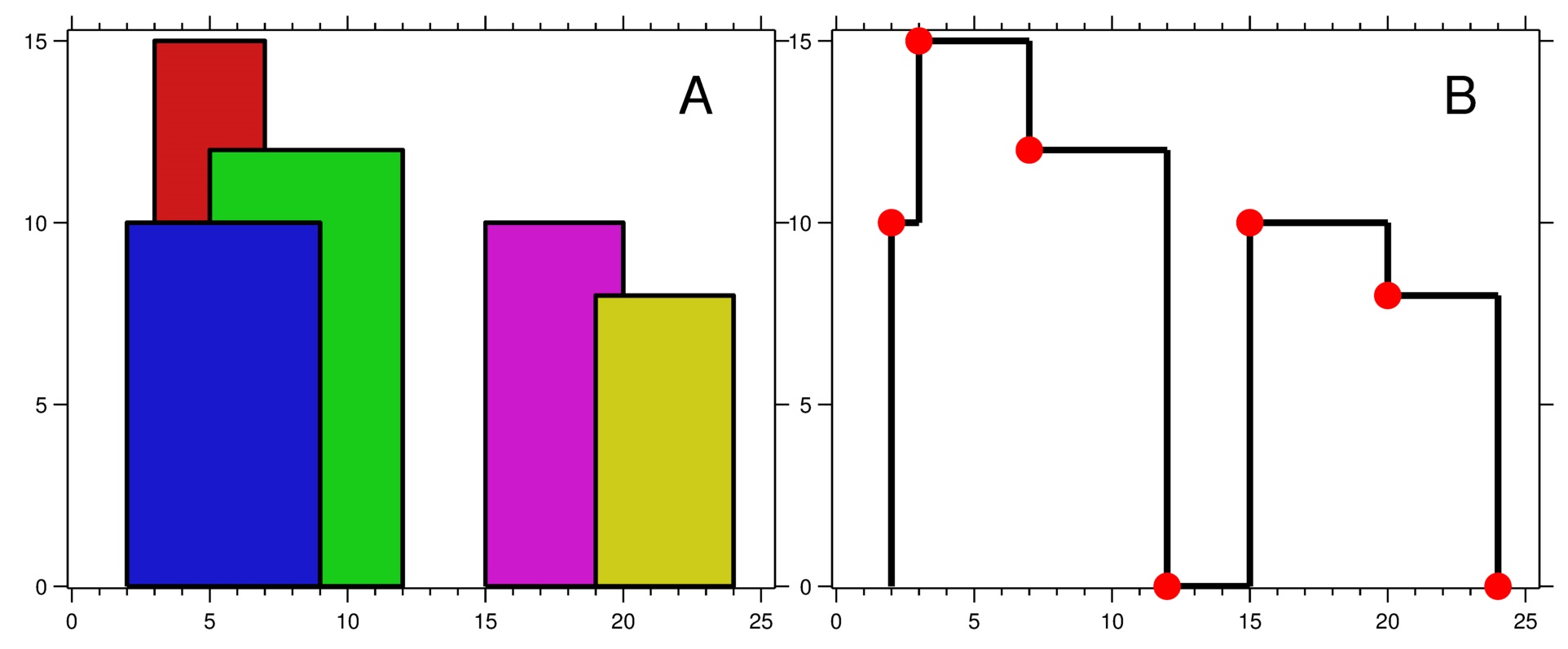
三、解題
Priority Queue
struct apk_info{
int apk_version;
int min_version = 1;
int max_version = INT_MAX;
apk_info(int ver, int mn, int mx){
this->apk_version = ver;
this->min_version = mn;
this->max_version = mx;
}
};
class Solution {
public:
unordered_map<int, int> waitList;
void remove(priority_queue<int>& pq, int item){
if (pq.top() == item) { // 若 pq 的頂是要移除的對象,則直接移除
pq.pop();
while (waitList.find(pq.top()) != waitList.end() && waitList[pq.top()] > 0) {
waitList[pq.top()]--;
pq.pop();
}
} else {
waitList[item]++; // 若 pq 的頂非要移除的對象,則加入 waitList,待之後再移除
}
}
vector<pair<int,int>> getRangeMax(vector<apk_info*> infos) {
vector<pair<int,int>> rangeMax, osVers;
for (const auto& info : infos) {
osVers.push_back({info->min_version, -info->apk_version}); // 以負值代表 skyline 的開始
osVers.push_back({info->max_version, info->apk_version}); // 以正值代表 skyline 的結束
}
sort(osVers.begin(), osVers.end()); // 以 x 值(os_version) 進行排序
priority_queue<int> pq;
pq.push(0); // not found 時,預設回傳 0
int prev = 0; // 在還沒插入 item 前一開始的最大值就是 0
for (const auto& osVer : osVers) {
if (osVer.second < 0){ // 開始
pq.push(-osVer.second);
} else { // 結束,需移除該點
remove(pq, osVer.second);
}
int curr = pq.top();
if (prev != curr) { // 若最大值有變,則需把 skyline 記錄下來
if (prev < curr || osVer.first == INT_MAX)
rangeMax.push_back({osVer.first, curr}); // x 軸為 os version,y 軸為 apk version
else // 為做成 [a, b) 左閉右開的區間,若 skyline 往下,x 軸的點位置需加 1 (版本以大的為主)
rangeMax.push_back({osVer.first+1, curr});
prev = curr;
}
}
return rangeMax;
}
public:
vector<int> findOSVersion(vector<apk_info*> infos, vector<int> queries) {
vector<pair<int,int>> rangeMax = getRangeMax(infos); // 以範例來說會回傳 [[1,2],[9,0],[12,3],[17,1],[INT_MAX, 0]]
vector<int> res;
for (const int& q : queries){
auto it = upper_bound(rangeMax.begin(), rangeMax.end(), make_pair(q, INT_MAX)); // 開區間找上限後,往前推一位
it--;
res.push_back(it->second);
}
return res;
}
};
// test case
int main(){
apk_info* a1 = new apk_info(1, 14, INT_MAX);
apk_info* a2 = new apk_info(2, 1, 8);
apk_info* a3 = new apk_info(3, 12, 16);
vector<apk_info*> infos = {a1, a2, a3};
vector<int> queries = {18,4,14,10}; // 1, 2, 3, 0
Solution* sol = new Solution();
vector<int> res = sol->findOSVersion(infos, queries);
for (int i = 0; i < res.size(); i++){
cout << res[i] << " ";
}
cout << endl;
return 0;
}
補充(segment tree)
- 用segment tree 來解區域更新的題目時,若把每個子葉點退化到單點的話,其空間複雜度會太高,可以用兩個 map 由左到右將 x 軸從小到大帶入,每個索引值 i 對應到一個有使用到的 x 軸座標。然後用左閉右開(\([a,b)\))的方式去維護區間的值。
- 在用segment tree 做區域更新時,若每次都對所有子葉做更新的話,其時間複雜度會拉高到\(O(k)\),\(k\) 為線段長。其下 slash 掉的部分,在 the skyline problem 中會造成 TLE,所以我們每次只對其必要的點做更新,待全部資料輸入完後,再一次從上而下做更新(renew)。其時間複雜度雜到\(O(klogk+n)\),\(n\) 為 x 軸的個數。
- 區域查詢也可以用差不多的概念完成。
class Solution {
class Tree {
vector<int> arr;
int m, n;
public:
Tree (int sz) {
n = sz;
for (m=1; m < n; m<<=1);
arr.assign(2*m, 0);
}
// void update(int b, int e, int val) {
// int i = b+m, j = e+m;
// for (; i && j && i <= j; i >>= 1, j >>= 1){
// for (int k = i; k <= j; k++){
// arr[k] = max(arr[k], val);
// }
// }
// }
// void renew(){}
void update(int b, int e, int val){
for (b+=m, e+=m; b <= e; b>>=1, e>>=1) {
if (b&1) arr[b++] = max(arr[b], val);
if (!(e&1)) arr[e--] = max(arr[e], val);
}
}
void renew() {
for (int i = 1; i < m; i++) {
arr[i<<1] = max(arr[i<<1], arr[i]);
arr[i<<1|1] = max(arr[i<<1|1], arr[i]);
}
}
int query(int i) {
return arr[i+m];
}
};
unordered_map<int,int> i2x, x2i;
public:
int mapping(vector<vector<int>>& buildings) {
set<int> sets;
for (const auto& building : buildings) {
sets.insert(building[0]);
sets.insert(building[1]);
}
int cnt = 0;
for (const auto& x : sets){
i2x[cnt] = x;
x2i[x] = cnt++;
}
return cnt;
}
vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
int n = mapping(buildings);
Tree* root = new Tree(n);
for (const auto& building : buildings) {
int b = x2i[building[0]];
int e = x2i[building[1]];
root->update(b, e-1, building[2]);
}
root->renew();
vector<vector<int>> res;
int prev = 0;
for (int i = 0; i < n; i++){
int x = i2x[i];
int y = root->query(i);
if (prev != y) {
res.push_back({x, y});
prev = y;
}
}
return res;
}
};