布林邏輯式的簡化# 卡諾圖(Karnaugh Maps, K-maps)是一種簡單、快速的簡化布林邏輯的方法。 SOP# 將布林邏輯化簡成最簡SOP(Minimum Sum of products)\(F=A’ B’ C’+A’ B’ C+A’ BC’+AB’ C+ABC’ +ABC\) \(F=A’ B’+B’ C+BC’+AB\) \(F=A’ B’+BC’+AC\) POS# 將布林邏輯化簡成最簡POS(Minimum Product of Sums)\(F=(A+B’+C+D’)(A+B’+C’+D’)(A+B’+C’+D)(A’+B’+C’+D)(A+B+C’+D)(A’+B+C’+D)\) \(F=(A+B’+D’)(A+B’+C’)(B’+C’+D)(B+C’+D)\) \(F=(A+B’+D)(A+B’+C’)(C’+D)\) \(F=(A+B’+D’)(C’+D)\) 2或3個變數的卡諾圖# 簡化2個變數的布林邏輯式# \(F=A’ B’+A’ B\)布林代數:\(F=A’ B’+A’ B=A’(B’+B)=A’\) 卡諾圖:\(
\boxed{
\def\arraystretch{1.4}\begin{array}{c|c|c}
\downarrow B\rightarrow A&0&1&\\\hline
0&\text{A=0,B=0}&\text{A=1,B=0}\\\hline
1&\text{A=0,B=1}&\text{A=1,B=1}\\
\end{array}
}
\rightarrow
\boxed{
\def\arraystretch{1.4}\begin{array}{c|c|c}
&A’&A&\\\hline
B’&1&0\\\hline
B&1&0\\
\end{array}
}
\rightarrow
A'
\) 簡化3個變數的布林邏輯式# \(F=\sum m(2,3,6)=A’ BC’+A’ BC+ABC’\)布林代數:\(F=A’ BC’+A’ BC+ABC’=A’ B+BC’\) 卡諾圖:*注意相鄰以grey code排列 \(
\boxed{
\def\arraystretch{1.4}\begin{array}{c|c|c}
\downarrow BC\rightarrow A&0&1&\\\hline
00&m_0(000)&m_4(100)\\\hline
01&m_1(001)&m_5(101)\\\hline
11&m_3(011)&m_7(111)\\\hline
10&m_2(010)&m_6(110)\\
\end{array}
}
\rightarrow
\boxed{
\def\arraystretch{1.4}\begin{array}{c|c|c}
&A’&A&\\\hline
B’ C’&0&0\\\hline
B’ C &0&0\\\hline
B C &1&0\\\hline
B C’ &1&1\\
\end{array}
}
\rightarrow
A’ B+BC'
\) 相鄰(Adjacency)的定義# 最上面可以與最下面相接,視為相鄰 最左邊可以與最右邊相接,視為相鄰\(
\boxed{
\def\arraystretch{1.4}\begin{array}{c|c|c}
&A’&A&\\\hline
B’ C’&0&0\\\hline
B’ C &0&0\\\hline
B C &1&1\\\hline
B C’ &0&0\\
\end{array}
}
\rightarrow BC
\) \(
\boxed{
\def\arraystretch{1.4}\begin{array}{c|c|c}
&A’&A&\\\hline
B’ C’&1&0\\\hline
B’ C &0&0\\\hline
B C &0&0\\\hline
B C’ &1&0\\
\end{array}
}
\rightarrow A’ C'
\) 組合的規則# 以組合相鄰 且以2為倍數 為規則 組合的元素愈多愈好 可以重複選(cover) 等效最簡式# \(\boxed{\def\arraystretch{1.4}\begin{array}{c|c|c}
&A’&A&\\\hline
B’ C’&1&0\\\hline
B’ C &1&1\\\hline
B C &0&1\\\hline
B C’ &1&1\\
\end{array}}
\rightarrow
F=A’ B’+BC’+AC=A’ C’+B’C+AB
\) 4個變數的卡諾圖# \(F=ACD+A’ B+D’\) 以卡諾圖表示\(\boxed{\def\arraystretch{1.4}\begin{array}{c|c|c|c|c}
&A’ B’&A’ B&AB&AB’\\\hline
C’ D’&1&1&1&1\\\hline
C’ D & &1& & \\\hline
C D & &1&1&1\\\hline
C D’ &1&1&1&1\\
\end{array}}
\quad
\boxed{\def\arraystretch{1.4}\begin{array}{c|c|c|c|c}
&00&01&11&10\\\hline
00&m_0&m_4&m_{12}&m_8\\\hline
01&m_1&m_5&m_{13}&m_9\\\hline
11&m_3&m_7&m_{15}&m_{11}\\\hline
10&m_2&m_6&m_{14}&m_{10}\\
\end{array}}
\) 以 min-term expression 方式解題# 解 \(F(a,b,c,d)=\sum m(1,3,4,5,10,12,13)\)\(
\boxed{\def\arraystretch{1.4}\begin{array}{c|c|c|c|c}
&00&01&11&10\\\hline
00& &1&1& \\\hline
01&1&1&1& \\\hline
11&1& & & \\\hline
10& & & &1\\
\end{array}}
\rightarrow
F=bc’+a’ b’ d+ab’ c’d
\) 考慮 Don’t care 的情況# 解 \(F(a,b,c,d)=\sum m(1,3,5,7,9)+\sum d(6,12,13)\)\(
\boxed{\def\arraystretch{1.4}\begin{array}{c|c|c|c|c}
&00&01&11&10\\\hline
00& & &X& \\\hline
01&1&1&X&1\\\hline
11&1&1& & \\\hline
10& &X& & \\
\end{array}}
\rightarrow
F=a’d+c’d
\) 以 max-term expression 方式解題# 解 \(F(a,b,c,d)=\sum m(0,2,3,4,8,10,11,15)=\prod M(1,5,6,7,9,12,13,14)\)\(
\boxed{\def\arraystretch{1.4}\begin{array}{c|c|c|c|c}
&00&01&11&10\\\hline
00& & &0& \\\hline
01&0&0&0&0\\\hline
11& &0& & \\\hline
10& &0&0& \\
\end{array}}
\) 基本質函項(essential prime implicants)# 名詞定義# 蘊函項(Implicant)任何可以被組合的單一或群元素(意指為 \(F\)的子集。) 質函項(Prime Implicant)已不能再被組合更多的函項。(意指最大的、框選最多的子集) 基本質函項(Essential Prime Implicant) \(
\boxed{\def\arraystretch{1.4}\begin{array}{c|c|c|c|c}
&00&01&11&10\\\hline
00& & &1& \\\hline
01&1&1&1& \\\hline
11& &1&1&1\\\hline
10& &1& & \\
\end{array}}
\)蘊函項:\(A’ C’ D, ABC’, ACD, A’ BC, BD, m_1, m_5, m_6, m_7…. \) 質函項:\(A’ C’ D, ABC’, ACD, A’ BC, BD \) 基本質函項:\(A’ C’ D,ABC’,A’ BC, ACD\) 簡化原則# 盡可能將式子展開成質函項(Prime implicants)。 用盡可能最少的質函項來表式布林函式。 例題 \(
\boxed{\def\arraystretch{1.4}\begin{array}{c|c|c|c|c}
&00&01&11&10\\\hline
00& &1&1& \\\hline
01&1&1&1& \\\hline
11&1& &1&1\\\hline
10& & &1&1\\
\end{array}}
\rightarrow
F=A’ B’ D+BC’+AC
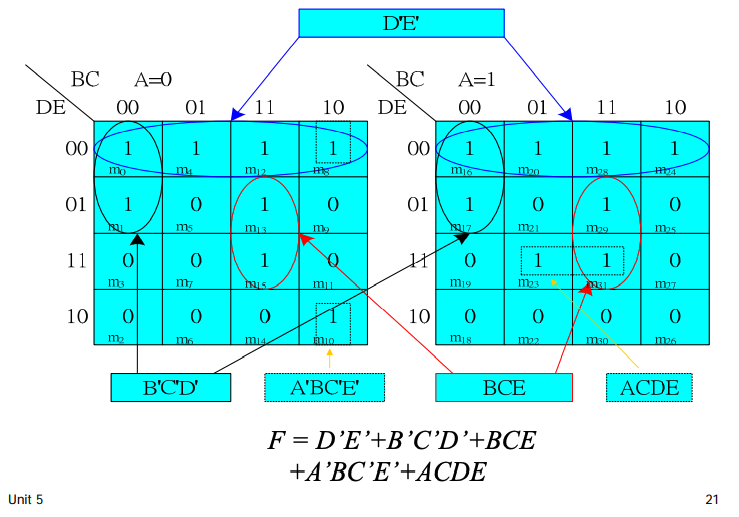
\) 5個變數的卡諾圖# 表示法1
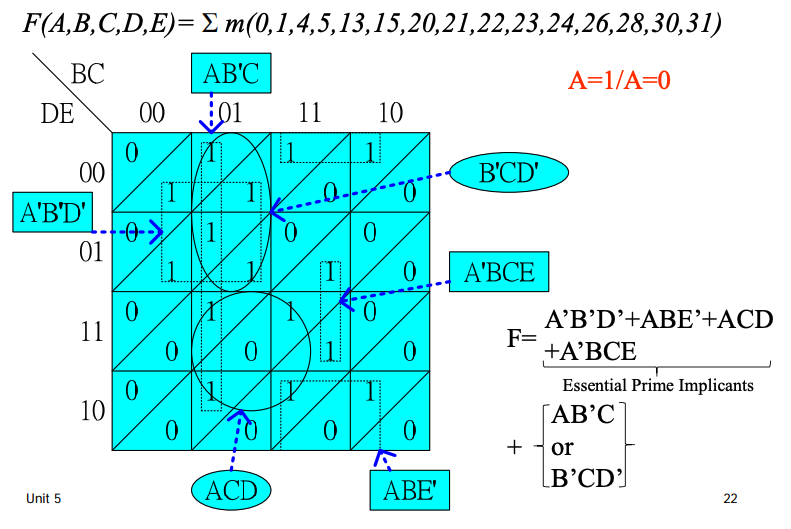
表示法2