線段樹 Segment Tree

簡介

線段樹是演算法中常用來維護區間訊息的資料結構。
空間複雜度為 \(O(n)\)，\(n\) 代表區間數。
查詢的時間複雜度為 \(O(\log n+k)\)，\(k\) 代表符合條件的區間數量。
線段樹將每個長度為為 1 的區間劃分為左右兩個區間遞迴求解，把整個線段劃分為一個樹型結構，通過合併左右兩個區間訊息來求得該區間的訊息。
在實現時，我們考慮遞迴建樹，設當前的根節點為 root，如果根節點管轄的區間長度已經是 1，則可以直接根據數組上相應位置的值初始化該節點。否則需將該區間從中點處分割為兩個子區間，分別進入左右子節點遞迴建樹，最後合併兩個子節點的訊息，

建樹 build

void build(int s, int t, int p, const vector<int>& arr){
    if (s == t){
        tree[p] = SegmentItem(arr[s], 1);
        return;
    }
    int m = s + ((t - s) >> 1);
    build(s, m, p*2, arr);
    build(m+1, t, p*2+1, arr);
    // push_up
    tree[p] = tree[p*2] + tree[(p*2)+1];
}

查詢 query

SegmentItem find(int l, int r, int s, int t, int p){
    if (l <= s && t <= r){
        return tree[p];
    }
    int m = s + ((t - s) >> 1);
    SegmentItem sum;
    if (r <= m) return find(l, r, s, m, p*2);
    if (l > m) return find(l, r, m+1, t, p*2+1);
    return find(l, r, s, m, p*2) + find(l, r, m+1, t, p*2+1);
}

zkw 線段樹

來自清華大學張昆瑋(zkw)-《統計的力量》
以非遞迴的方式構建，效率更高，程式更短。
普通的線段樹是從上到下做處理，容易定位根節點，卻不容易定位子節點。
zkw 線段樹是當二叉樹是滿二叉樹時，因為子節點的編號具有以下規律：
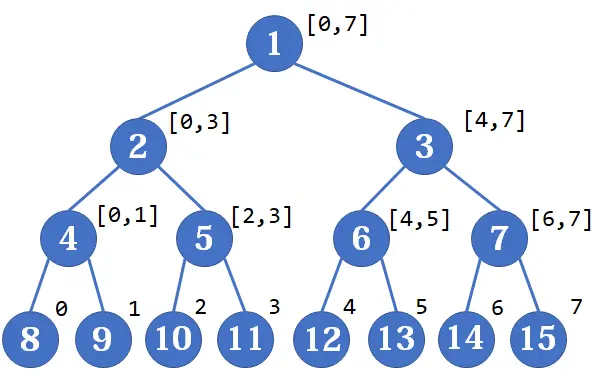
- 葉子節點(left) 全部退化為線段 \([x,x]\) 。
- \(n\) 個數據點則取大於等 \(n\)且為 \(2\) 的冪次的兩倍作為數組大小。 \((m=2^a\ge n)\)
```
for (int m = 1; m <= n; m >>= 1)
```
- 維護點為 \(n\) 個。索引為\([m,m+n)\)。
- 子葉數目為 \(m\) 個。索引為\([m,2m)\)
- 節點數為 \(2m-1\) 個。(數組大小需設 \(2m\) 因為 zkw tree是 1-index的)
- 樹高 \(H=\log_2(m)+1\) 層。
  - 第 \(h\) 層有 \(2^{h-1}\) 個節點，
  - 該層線段長度為 \(2^{H-h}\)。
- 若某節點為 \(p\)，父節點為 \(p/2\)，子節點為 \(2p\) 和 \(2p+1\)
```
int parent = p >> 1;
int left = p << 1;
int right = p << 1 | 1;
```
- 若兩節點為 \(p\) 與 \(q\)，且兩節點互為兄弟節點，則 \(p\oplus q=1\)
```
if (left ^ right)
    // left 與 right 為兄弟節點
else
    // left 與 right 不為兄弟節點
```
- 除根節點外，左節點皆為偶數，右節點皆為奇數
```
if (i == 1)
    // i 為根節點
else if (i & 1)
    // i 為奇數，為右節點
else if (!(i & 1))
    // i 為偶數，為左節點
```

結構

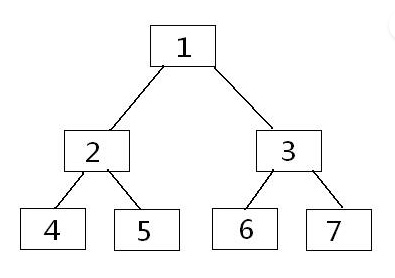
線段樹索引堆疊：
轉成二進制：
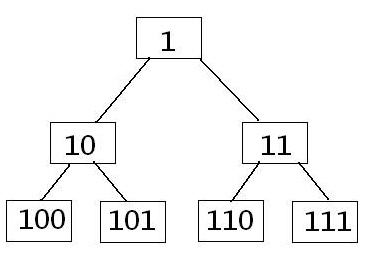
規律：
- 一個節點的父節點是該數右移 1，低位捨棄。
- 一個節點的左子節點是該數左移 1，右子節點是該數左移 1 再加 1。
- 同一層的節點是依次遞增的，第 \(n\) 層有 \(2^{n-1}\)個節點
- 最後一層有多少個節點，值域就是多少。

建樹 build

取 m 值有許多版本，有些版本會直接取 \(m=2^{log_2(n+5)+1}\)以節省迭代計算
- 寫成 int n = 1 << __lg(n+5)+1;
可以有開區間與閉區間兩種做法，差別在於從子葉節點的最左邊 \(m+i\) 開始，或是第二個子葉節點 \(m+1+i\) 開始。
由下而上更新時，開區間與閉區間的終止條件不同：
- 開區間的終止條件為兩子節點互為兄弟節點
```
while (i^j^1)
    // operation
```
- 閉區間的終止條件為右節點小於左節點
```
while (i <= j)
    // operation
```

class Tree {
private:
    vector<int> arr;
    int n, m;   // n 為維護點數, m 為 zkw-tree 子葉節點數
public: 
    Tree (vector<int>& nums){
        n = nums.size();
        for (m = 1; m <= n; m <<= 1);   // 取大於等於 n 且為 2 的冪次的最小整數
        arr.assign(2*m, 0);     // 節點數設為 2m 個，其中 0 為空節點
    }
    void build(vector<int> nums){
        for (int i = 0; i < n; i++) {
            arr[i+m] = nums[i];  // 從子葉節點最左邊往右更新節點。
            mx[i+m] = nums[i];
            mn[i+m] = nums[i];
        }
        for (int i = m-1; i; i--){  // 向上更新父節點。
            arr[i] = in(x);
        }
    }
};

根據不同需求代換 \(\text{in(x)}\)：取和、最大值、最小平

    // 取和
    arr[i] = arr[i<<1] + arr[i<<1|1];
    // 取最大值
    arr[i] = max(arr[i<<1], arr[i<<1|1]);
    // 取最小值
    arr[i] = min(arr[i<<1], arr[i<<1|1]);

更新 update

單點修改(以和為例)
更新時，以差分方式，將所有父節點加上更新點的差值。

void update(int i, int val){
    int diff = val - arr[m+i]   // 原值 arr[m+i] 與新值 val 的差
    for (i += m; i; i >>= 1){
        arr[i] += diff;
    }
}

查詢 query

單點查詢(以和為例)：閉區間做法
判斷左邊界是否為右節點，若為右節點則加上後往右邊的父節點移動。
判斷右邊界是否為左節點，若為左節點則加上後往左邊的父節點移動。

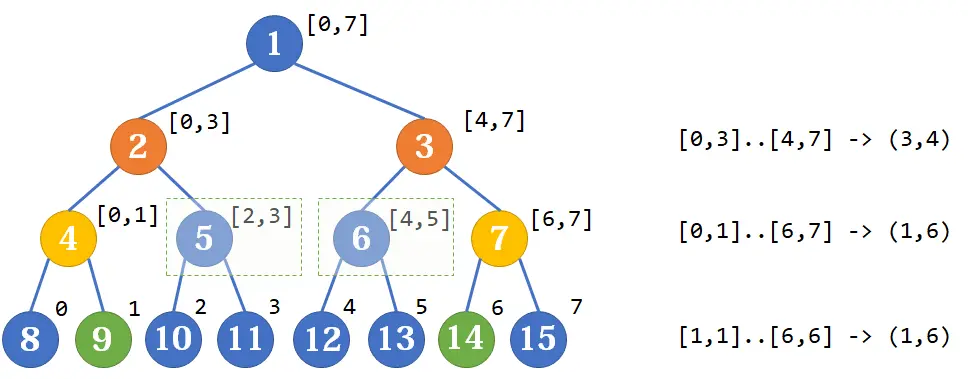
int query(int left, int right){
    int sum = 0;
    int i = left+m;     // 左閉區間
    int j = right+m;    // 右閉區間
    for (; i <= j; i >>= 1, j >>= 1){
        if (i & 1) sum += arr[i++];
        if (!(j & 1)) sum += arr[j--];
    }
    return sum;
}

備註：開區間作法 (0-index 時會出現 -1 的情形，建議使用閉區間)

int query(int left, int right){
    int sum = 0;
    int i = left+m-1;
    int j = right+m+1;
    for(; i^j^1; i >>= 1, j >>= 1){
        if (~i & 1) sum += arr[i^1];
        if (j & 1) sum += arr[j^1];
    }
    return sum;
}

區間修改

在非遞迴的情況下，標記下傳是比較困難的，所以作法上改成將標記永久化。
具體而言，與查詢類似，當左端點是左子節點且右端點是右子節點時，我們對它的兄弟節點進行修改並標記，表示這顆子樹中的每個節點都要被修改。但單純這樣還不夠，因上述修改還會波及到這些節點的各級祖先，所以我們需要在途中根據實際修改的區間長度來更新各級祖先的值，這種操作需要一路上推到根節點。 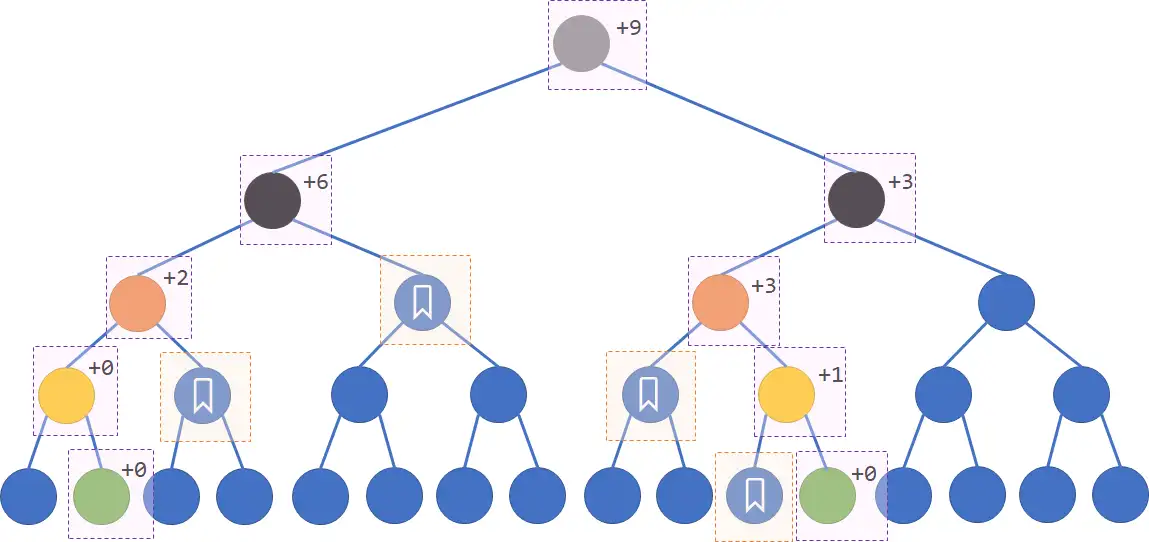(開區間作法)

void update(int left, int right, int diff){
    int len = 1, cntl = 0, cntr = 0; // cntl, cntr 是左右邊分別實際修改的區間長度
    left += m-1;
    right += m+1;
    for (; left^right^1; left >> 1, right >> 1, len << 1){
        arr[left] += cntl * diff;
        arr[right] += cntr * diff;
        if (~left & 1) {
            arr[left^1] += diff * len;
            mark[left^1] += diff;
            cntl += len;
        }
        if (right & 1) {
            arr[right^1] += diff * len;
            mark[right^1] += diff;
            cntr += len;
        }
    }
    for (; left; left >>= 1, right >>= 1){
        arr[left] += cntl * diff;
        arr[right] += cntr * diff;
    }
}

在有區間修改存在時，區間查詢也需要考慮標記的影響。
所以除了加上端點的兄弟節點訊息，沿途中遇到的標記也對答案有貢獻，同樣需要上推到根節點。

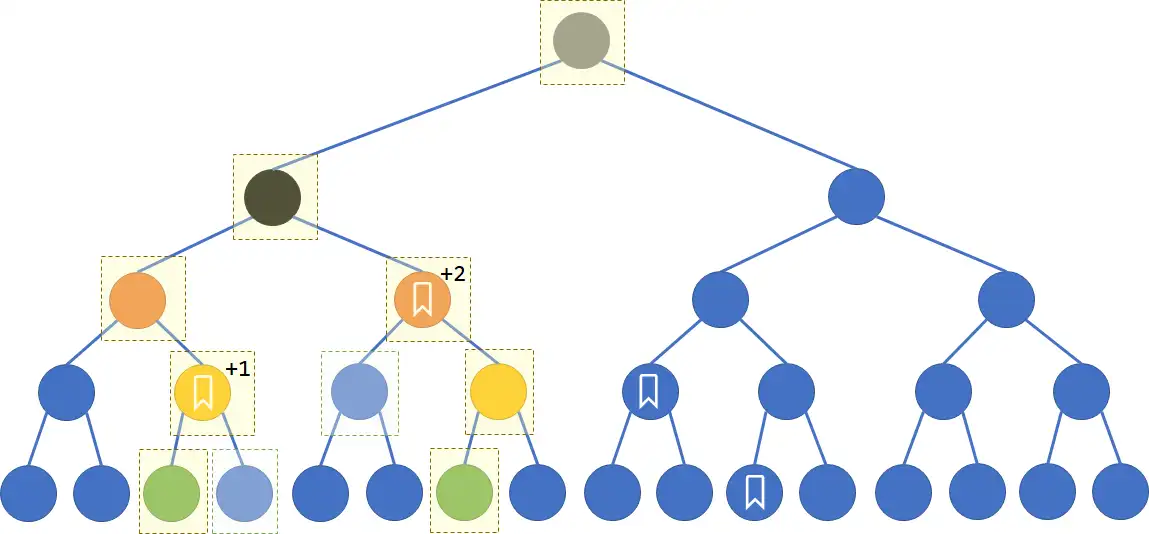
int query(int left, int right){
    int sum = 0, len = 1, cntl = 0, cntr = 0;
    left += m - 1;
    right += m + 1;
    for (; left^right^1; left >>= 1, right >>= 1, len << 1){
        sum += cntl * mark[left] + cntr * mark[right];
        if (~left & 1) sum += arr[left^1], cntl += len;
        if (right & 1) sum += arr[right^1], cntr += len;
    }
    for (; left; left >> 1, right >> 1){
        sum += cntl * mark[left] + cntr * mark[right];
    }
    return sum;
}

區間查詢最大值：

void update(int l, int r, int d) {
    for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
    {
        if (l < N) tree[l] = max(tree[l << 1], tree[l << 1 | 1]) + mark[l],
                    tree[r] = max(tree[r << 1], tree[r << 1 | 1]) + mark[r];
        if (~l & 1) tree[l ^ 1] += d, mark[l ^ 1] += d;
        if (r & 1) tree[r ^ 1] += d, mark[r ^ 1] += d;
    }
    for (; l; l >>= 1, r >>= 1)
        if (l < N) tree[l] = max(tree[l << 1], tree[l << 1 | 1]) + mark[l],
                    tree[r] = max(tree[r << 1], tree[r << 1 | 1]) + mark[r];
};
int query(int l, int r) {
    int maxl = -INF, maxr = -INF;
    for (l += N - 1, r += N + 1; l ^ r ^ 1; l >>= 1, r >>= 1)
    {
        maxl += mark[l], maxr += mark[r];
        if (~l & 1) cmax(maxl, tree[l ^ 1]);
        if (r & 1) cmax(maxr, tree[r ^ 1]);
    }
    for (; l; l >>= 1, r >>= 1)
        maxl += mark[l], maxr += mark[r];
    return max(maxl, maxr);
};

Leetcode. 307 範例

https://leetcode.com/problems/range-sum-query-mutable/

TreeNode 變形

class NumArray {
    class SegTree {
    public:
        int val;
        int begin, end;
        SegTree* left, *right;
        SegTree(int v):val(v) {}
        SegTree(int v, int b, int e):val(v), begin(b), end(e) {}
        SegTree(int v, int b, int e, SegTree* l, SegTree* r)
            :val(v), begin(b), end(e), left(l), right(r) {}
    };
    
    SegTree* root;
    
    SegTree* build(vector<int>& nums, int b, int e){
        if (e < b) return NULL;
        if (b == e) return new SegTree(nums[b], b, b);
        int mid = b + (e-b)/2;
        SegTree* left = build(nums, b, mid);
        SegTree* right = build(nums, mid+1, e);
        return new SegTree(left->val + right->val, b, e, left, right);
    }
    
    void update(SegTree* node, int index, int val){
        if (node->begin == index && node->end == index){
            node->val = val;
        } else {
            int mid = node->begin + (node->end - node->begin)/2;
            if (index <= mid){
                update(node->left, index, val);
            } else {
                update(node->right, index, val);
            }
            node->val = node->left->val + node->right->val;
        }
    }
    int query(SegTree* node, int left, int right){
        if (node->begin == left && node->end == right){
            return node->val;
        }
        int mid = node->begin + (node->end - node->begin)/2;
        if (right <= mid){
            return query(node->left, left, right);
        } else if (left > mid){
            return query(node->right, left, right);
        }
        return query(node->left, left, mid) + query(node->right, mid+1, right);
    }
    
public:
    NumArray(vector<int>& nums) {
        root = build(nums, 0, nums.size()-1);
    }
    
    void update(int index, int val) {
        update(root, index, val);
    }
    
    int sumRange(int left, int right) {
        return query(root, left, right);
    }
};

zkw 線段樹

class NumArray {
    class SegTree {
        vector<int> arr;
        int m, n;
    public:
        SegTree(vector<int>& nums) {
            n = nums.size();
            for (m = 1; m < n; m <<= 1);
            build(nums);
        }
        void build(vector<int>& nums) {
            arr.assign(2*m, 0);
            for (int i = 0; i < n; ++i) arr[m+i] = nums[i];
            for (int i = m-1; i; --i) arr[i] = arr[i<<1] + arr[i<<1|1];
        }
        void update(int index, int val) {
            int diff = val - arr[m+index];
            for (index += m; index; index >>= 1) arr[index] += diff;
        }
        int query(int left, int right) {
            int sum = 0;
            for (int i = left+m, j = right+m; i <= j; i >>= 1, j >>= 1){
                if (i & 1) sum += arr[i++];
                if (!(j & 1)) sum += arr[j--];
            }
            return sum;
        }
    };
public:
    SegTree* root;
    NumArray(vector<int>& nums) {
        root = new SegTree(nums);
    }
    
    void update(int index, int val) {
        root->update(index, val);
    }
    
    int sumRange(int left, int right) {
        return root->query(left, right);
    }
};

BIT(binary indexed tree)

class NumArray {
public:
    class Bit {
    public:
        vector<int> bit;
        int n;
        Bit(vector<int>& nums) {
            n = nums.size();
            bit.assign(n+1, 0);
            for (int i = 0; i < n; i++){
                build(i+1, nums[i]);
            }
        }
        void build(int index, int val) {
            while (index <= n){
                bit[index] += val;
                index = next(index);
            }
        }
        int next(int index) {
            return index + (index & -index);
        } 
        int parent(int index) {
            return index - (index & -index);
        }
        int getSum(int index) {
            int sum = 0;
            while (index){
                sum += bit[index];
                index = parent(index);
            }
            return sum;
        }
    };
    Bit* bit;
    NumArray(vector<int>& nums) {
        bit = new Bit(nums);
    }
    
    void update(int index, int val) {
        int diff = val - sumRange(index, index);
        bit->build(index+1, diff);
    }
    
    int sumRange(int left, int right) {
        return bit->getSum(right+1) - bit->getSum(left);
    }
};

線段樹 Segment Tree#

簡介#

建樹 build#

查詢 query#

zkw 線段樹#

結構#

建樹 build#

更新 update#

查詢 query#

區間修改#

Leetcode. 307 範例#

BIT(binary indexed tree)#

線段樹 Segment Tree

簡介

建樹 build

查詢 query

zkw 線段樹

結構

建樹 build

更新 update

查詢 query

區間修改

Leetcode. 307 範例

BIT(binary indexed tree)