一、Big O 表示法# Big O 的數學定義:
\(\boxed{O(g(n)) = \lbrace{f(n):存在正常量\space c\space 和\space n_0,使得對所有\space n\ge n_0,有\space 0 \le f(n) \le cg(n)\rbrace}}\) 我們常用的 big O 表示法中的 \(O\) 其實代表了一個函數的集合,比方說 \(O(n^2)\) 代表著一個由 \(g(n) = n^2\) 派生出來的一個函數集合;我們說一個演算法的時間複雜度為 \(O(n^2)\),意思就是描述該演算法的複雜度函數屬於這個函數集合之中。 分析複雜度時,常用的兩個特性:只保留增長速率最快的項,其它省略 \(\boxed{O(2n+100) = O(n)}\) \(\boxed{O(2^{n+1}) = O(2^n)}\) \(\boxed{O(m+3n+99) = O(m+n)}\) \(\boxed{O(n^3+999\times n^2+999\times n) = O(n^3)}\) Big O 記號表示複雜度的「上限」 換句話說,只要給出的是一個上限,用 Big O 表示法都是正確的。 但在習慣上,我們特別取最緊臨的上限。但若複雜度會跟算法的輸入數據有關,沒辦法提前給出一個特別精確的時間複雜度時,擴大時間複雜度的上限就變得有意義了。
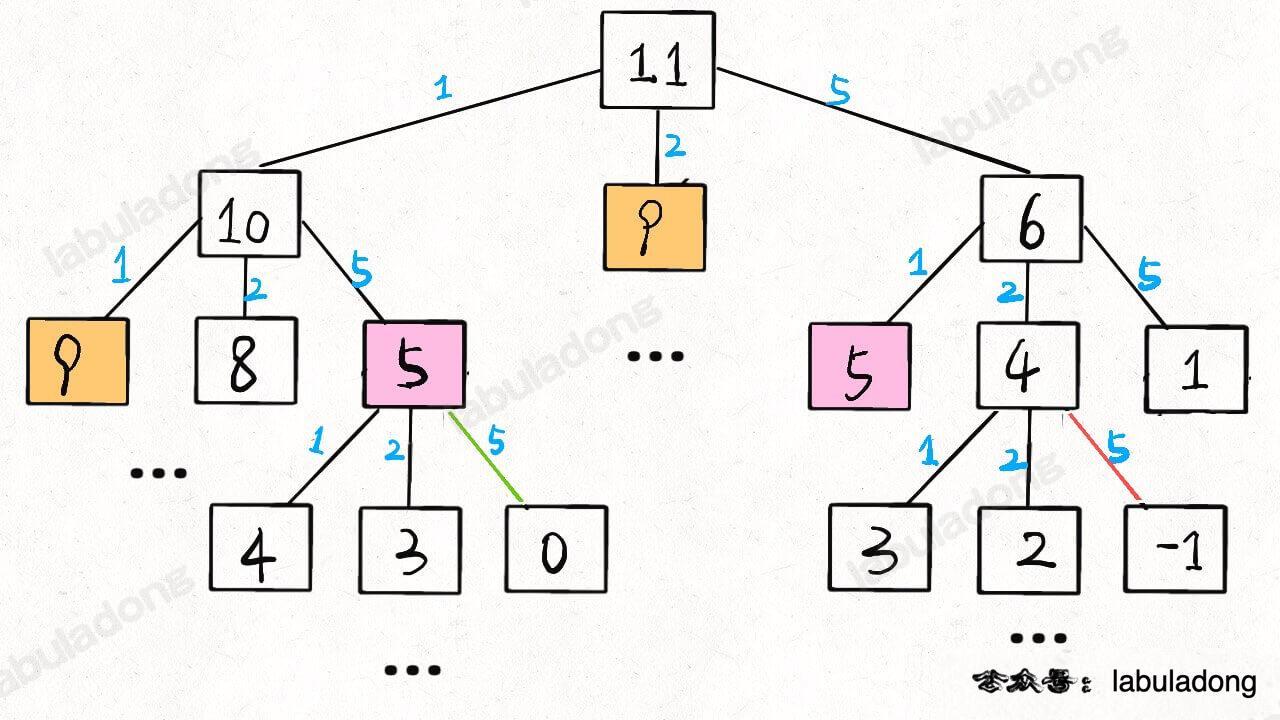
例如湊零錢問題中,金額 amount 的值為 n,coins 列表中的個數為 k,則這棵遞迴樹就是 K 叉樹。而節點的數量與樹的結構有關,而我們無法提前知道樹的結構,所以我們按照最壞情形來處理,高度為 n 的一棵滿 k 叉樹,其節點數為 \(\frac{k^n-1}{k-1}\),用 big O 表示就是 \(O(k^n)\)。 二、主定理(Master Theorem)# 有時候時間複雜度的判斷沒那麼容易,主定理是一個數學推導的方法:可以參考網站https://brilliant.org/wiki/master-theorem/