一、資料結構概要
- 資料結構的存儲方式大體上只分為兩種: Array、Linked List。
雖說資料結構有 disjoint matrix, queue, stack, tree, graph 等等,但它們都可以視為 Array 與 Linked List 的上層結構,可以看成是以 Array 或 Linked List 為基底上的操作,只是 API 不同而已。- Array:由於是緊湊連續儲存的,可以隨機訪問,通過 index 快速找到對應元素,且相對節約空間。但也因必須一次性分配儲存空間,所以 array 如果需要擴充容量,就必須再重新分配一塊更大的空間,再把數孛複製過去,其時間複雜度為 \(O(N)\);在 array 中間進行 delete 與 insert,必須搬移後面所有數據以保持連續,故時間複雜度也為\(O(N)\)。
- Linked List:因為元素不連續,而是靠指針指向下一個元素的位置,所以不存在 array 的擴充容量的問題,如果知道某一元素的前一個節點與後一個節點,操作指針即可刪除該元素或者插入新元素,時間複雜度為\(O(1)\)。但正因為儲存空間不連續,無法根擇 index 算出對應元素的地址,所以不能隨機訪問;而且由於每個元素必須額外儲存前後元素位置的指針,相對較耗空間。
- 在 C、C++ 語言中,指針(pointer)的存在使得其能更直接對儲存空間的位址做操作,所以在處理 C 語言時,要額外了解指針的運作方式。
二、資料結構的基本操作
- 資料結構的基本操作不外乎: 遍歷(traverse)、增減查改(CRUD, create, read, update, delete)
- Array:數組的遍歷框架 -> 典型的線性迭代結構:
void traverse(vector<int> arr){ for (int i = 0; i < arr.size(); i++){ // iteration } }- ListNode:鏈表的遍歷框架 -> 兼具迭代與遞迴
由上述兩種基底可推廣至各種結構:class ListNode { public: int val; ListNode* next; }; void traverse(ListNode* head){ for (ListNode curr = head; curr != NULL; curr = curr->next){ // iteration } } void traverse(ListNode* head){ // recursion traverse(head->next); }- 二叉樹(Binary Tree)
class TreeNode { public: int val; TreeNode* left, right; }; void traverse(TreeNode* root){ traverse(root->left); traverse(root->right); }- N 叉樹(N-ary Tree)
class TreeNode { public: int val; vector<TreeNode*> children } void traverse(TreeNode* root){ for (TreeNode* child : root->children){ traverse(child); } }- 圖(graph):可視為 N 叉樹的結合體,再利用 visited 處理環(circle)
class Node { public: int val; vector<Node*> neighbors; } unordered_set<Node*> visited; // 處理已拜訪過的節點 void traverse(Node* node){ if (visited) return; // 檢查是否拜訪過了 visited.insert(node) // 將現在拜訪的節點標記成已拜訪的節點 for (TreeNode* neighbor : neighbors){ traverse(neighbor) } }
三、前序(pre-order)、中序(in-order)、後序(post-order)
- 在開始複雜的演算法前,重點在於熟悉如何處理不同的結構,並採用基礎的解題策略。
- 前序、中序、後序指的是遍歷一棵二元樹的方式。
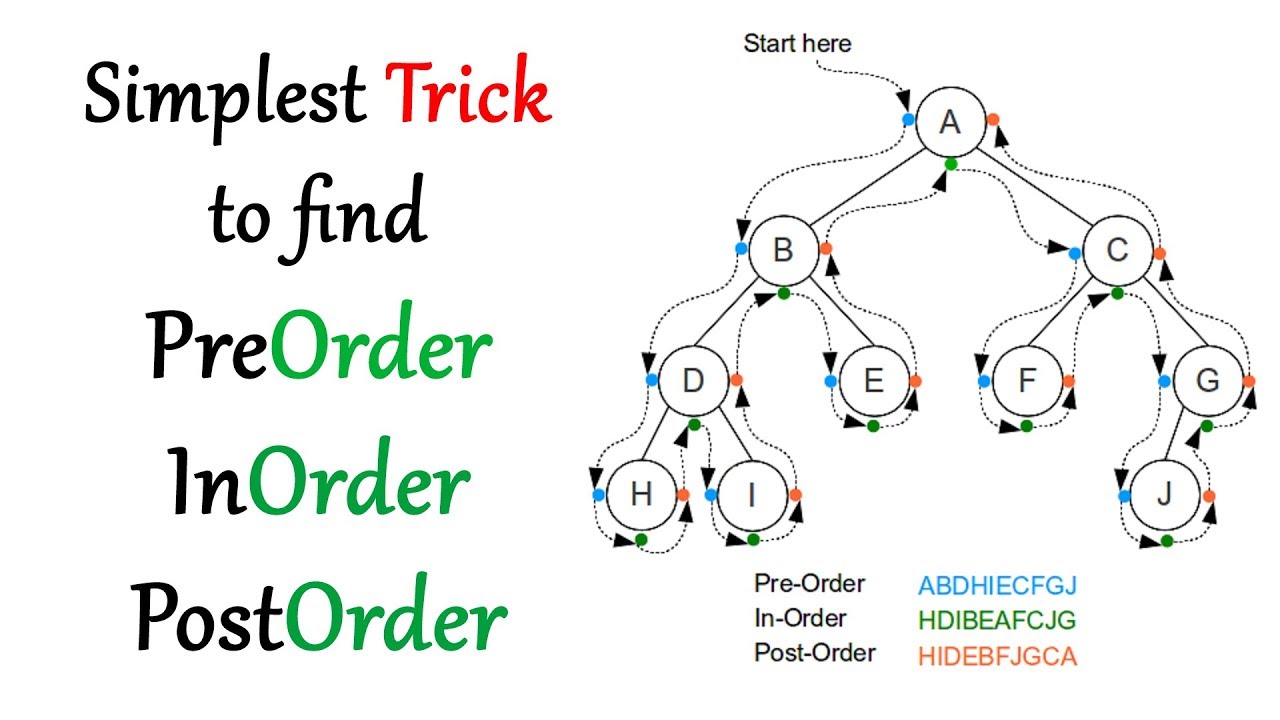
- 基本框架
void traverse(TreeNode* root){ // pre-order traverse(root->left); // in-order traverse(root->right); // post-order } - 鏈表其實也可以有前序、後序的關係:
void traverse(ListNode* curr){ // pre-order traverse(curr->next); // post-order }
