1026. Maximum Difference Between Node and Ancestor

  • Hardness: \(\color{orange}\textsf{Medium}\)
  • Ralated Topics: Tree、Depth-First Search、Binary Tree

一、題目

Given the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val - b.val| and a is an ancestor of b.
A node a is an ancestor of b if either: any child of a is equal to b or any child of a is an ancestor of b.

Example 1: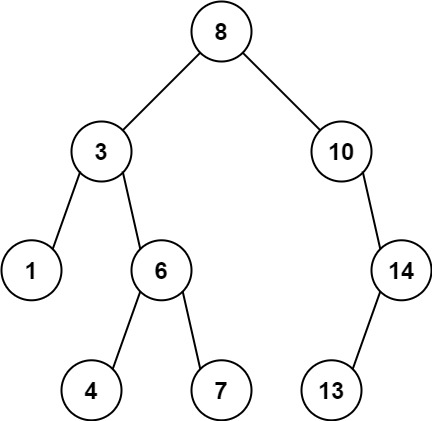
tmp-tree

  • Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
  • Output: 7
  • Explanation: We have various ancestor-node differences, some of which are given below :
    |8 - 3| = 5
    |3 - 7| = 4
    |8 - 1| = 7
    |10 - 13| = 3
    Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

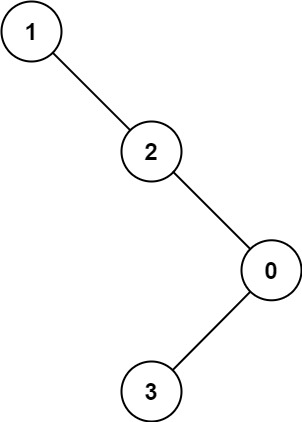
Example 2: tmp-tree-1

  • Input: root = [1,null,2,null,0,3]
  • Output: 3

Constraints:

  • The number of nodes in the tree is in the range [2, 5000].
  • 0 <= Node.val <= 10^5

二、分析

  • 借用一個 helper 函式，將父節點的值往子葉節點傳，並且記錄過程中的最大值與最小值，並定義一個全域變數記錄其差值。

三、解題

1. DFS

  • Time complexity: \(O(n)\)
  • Space complexity: \(O(1)\)
int res = 0;
int maxAncestorDiff(TreeNode* root) {
    helper(root, root->val, root->val);
    return res;
}
void helper(TreeNode* root, int maxv, int minv) {
    if (!root) return;
    maxv = max(maxv, root->val);
    minv = min(minv, root->val);
    helper(root->left, maxv, minv);
    helper(root->right, maxv, minv);
    res = max(res, maxv-minv);
}

回目錄 Catalog