938. Range Sum of BST
- Hardness: \(\color{green}\textsf{Easy}\)
- Ralated Topics:
Tree、Depth-First Search、Binary Search Tree、Binary Tree
一、題目
Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
Example 1: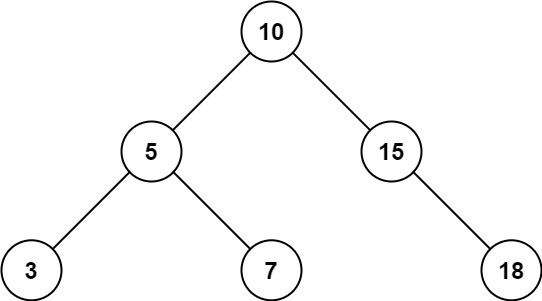
- Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
- Output: 32
- Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.
Example 2:
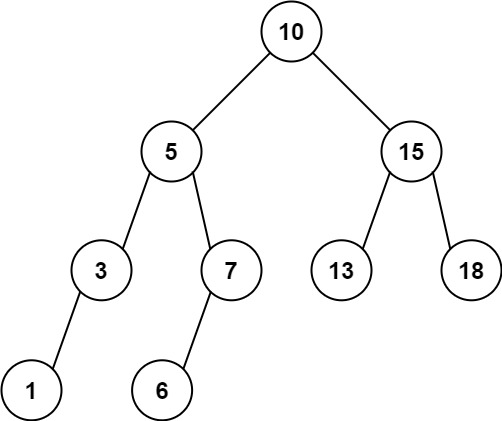
- Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
- Output: 23
- Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.
Constraints:
- The number of nodes in the tree is in the range
[1, 2 * 104]. 1 <= Node.val <= 1051 <= low <= high <= 105- All
Node.valare unique.
二、分析
- 最簡單的方法可以遍歷過一次,將符合條件的數值加起來,可得到解。
- 進一步可以思考,可以怎麼樣做到剪枝(pruning)。
- 當
num < low時,只有其右子葉有可能有符合條件的子葉。 - 當
num > high時,只有其左子葉有可能有符合條件的子葉。
- 當
三、解題
1. DFS
- Time complexity: \(O(n)\)
- Space complexity: \(O(1)\)
int rangeSumBST(TreeNode* root, int low, int high) {
if (!root) return 0;
int sum = root->val <= high && root->val >= low ? root->val : 0;
return sum + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high);
}
2. Binary Search Tree
- Time complexity: \(O(n)\)
- Space complexity: \(O(1)\)
int rangeSumBST(TreeNode* root, int low, int high) {
if (!root) return 0;
int val = root->val >= low && root->val <= high ? root->val : 0;
int left = root->val < low ? 0 : rangeSumBST(root->left, low, high);
int right = root->val > high ? 0 : rangeSumBST(root->right, low, high);
return left + right + val;
}