數位系統與開關電路#
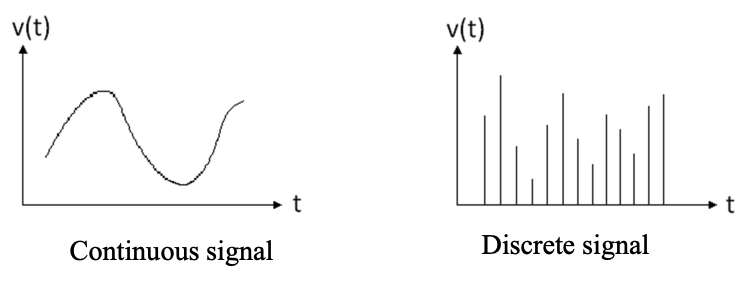
- 在現實世界中,資訊是以類比(Analog)的方式傳遞的,換言之,資訊是連續的
- 在電腦世界中,資訊是以數位(Digital)的方式傳遞的,也就是開與關或是0或1。
- A/D <-> DSP(digital signal processor) <-> D/A
Switching Circuit#
- 可分為三個層級:
- System: 模組Modules、算術運算單元 ALU(Arithmetic logic unit)、記憶體 Memory
- Logic:邏輯閘(gates)
- Circuit:電晶體(transistors)
- 經由 switching network 的設計,可將輸入轉成合乎 spec 的輸出。其中 switching network 的種類包含:
- Combinational network
- Sequential network
- 輸出是輸入的函數,可以表達當下的值或是過去的值。
- 具有記憶體的行為
- Switches
- 由電晶體來實現
- transistor level, gate level, module level…
數字系統與轉換#
- 在現實世界中,最普遍使用的數字系統為十進制(Decimal)
- 然而在電腦世界中,因為只有代表開與關的 0 與 1,故使用的數字系統是以二進制(Binary)為基礎。
- \(N=(a_2a_1a_0)_R=a_2\times R^2+a_1\times R^1+a_0\times R^0\)
| N | 正數表示 | -N | 正數加負號 | 1的補數 | 2的補數 |
|---|
| +0 | 0000 | -0 | 1000 | 1111 | N/A |
| +1 | 0001 | -1 | 1001 | 1110 | 1111 |
| +2 | 0010 | -2 | 1010 | 1101 | 1110 |
| +3 | 0011 | -3 | 1011 | 1100 | 1101 |
| +4 | 0100 | -4 | 1100 | 1011 | 1100 |
| +5 | 0101 | -5 | 1101 | 1010 | 1011 |
| +6 | 0110 | -6 | 1110 | 1001 | 1010 |
| +7 | 0111 | -7 | 1111 | 1000 | 1001 |
| +8 | N/A | -8 | N/A | N/A | 1000 |
二進制算數#
- 當兩數相加或兩數相減時,超過可用bits數時會發生overflow,
- 例如
-3+-4=-4是OK的 - 但
-5+-6=-11會產生溢位
二進制的表達方式 Binary codes#
| Decimal Digit | 8421 Code(BCD) | 6311 Code | Excess-3 Code | 2-out-of-5 Code | Gray Code |
|---|
| 0 | 0000 | 0000 | 0011 | 00011 | 0000 |
| 1 | 0001 | 0001 | 0100 | 00101 | 0001 |
| 2 | 0010 | 0011 | 0101 | 00110 | 0011 |
| 3 | 0011 | 0100 | 0110 | 01001 | 0010 |
| 4 | 0100 | 0101 | 0111 | 01010 | 0110 |
| 5 | 0101 | 0111 | 1000 | 01100 | 1110 |
| 6 | 0110 | 1000 | 1001 | 10001 | 1010 |
| 7 | 0111 | 1001 | 1010 | 10010 | 1011 |
| 8 | 1000 | 1011 | 1011 | 10100 | 1001 |
| 9 | 1001 | 1100 | 1100 | 11000 | 1000 |
Weighted Codes#
- 8421 Code 與 6311 都是 Weighted Code,代表每4個bit,各自代表的數字,
- 例:1011 for 8421 = 8 + 0 + 2 + 1 = 11
- 例:1011 for 6311 = 6 + 0 + 1 + 1 = 8
Excess-3 Codes#
- Excess-3 是以 8421 Code 為基礎下,額外加 3。
- 使得 i 與 10-i 互為 1 的補數,
- 0 與 9 為補數。(0011 與 1100)
- 1 與 8 為補數。(0100 與 1011)
- 2 與 7 為補數。(0101 與 1010)
- 3 與 6 為補數。(0110 與 1001)
- 4 與 5 為補數。(0111 與 1000)
Gray Codes#
- 兩相鄰的數只會相差一個 bit
- 又名 Reflected Binary Codes(RBC)、Unit distance code、Minimum error code
- 可以減少 switching operation
- 如何轉換 Gray Code? 參考Leetcode no.89
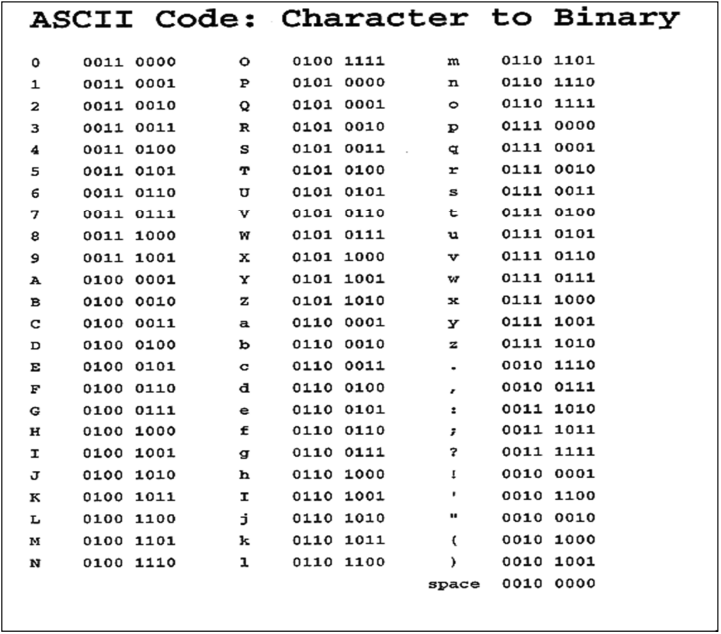
ASCII table#