布林表達式的轉換

  • 將文字敘述轉換成布林表達式：

\( \def\arraystrecth{1.5}\begin{array}{l} \underbrace{\text{The alarm will ring}}_ {Z} \text{ iff } \underbrace{\text{the power of alarm is on}} _{A} \text{ and } \underbrace{\text{the door is not closed}} _{B’} \\ \text{ or } \underbrace{\text{it is after 6 p.m.}} _{C} \text{ and } \underbrace{\text{the window is not closed}} _{D’} \end{array} \)

  • \(Z=AB’+CD’\)

由真值表開始建構邏輯電路

  • Truth Table:
    \( \boxed{ \def\arraystretch{1}\begin{array}{ccc|c|c} A&B&C&f&f’\\\hline 0&0&0&0&1\\ 0&0&1&0&1\\ 0&1&0&0&1\\ 0&1&1&1&0\\ 1&0&0&1&0\\ 1&0&1&1&0\\ 1&1&0&1&0\\ 1&1&1&1&0 \end{array} } \)
  • 利用 1’s 的函數
    \(f=A’ BC+AB’ C’+AB’ C+ABC’+ABC\)
    \(=A’ BC+AB’+AB\)
    \(=A’ BC+A\)
    \(=A+BC\)
  • 利用 0’s 的函數
    \(f=(A+B+C)(A+B+C’)(A+B’+C)\)
    \(=(A+B)(A+B’+C)\)
    \(=A+B(B’+C)\)
    \(=A+BC\)

Minterm 與 maxterm 展開

  • 以 \(F=A’ BC+A\) 為範例 \( \boxed{ \def\arraystretch{1}\begin{array}{c|ccc|c|c|cc} \text{Row No.}&A&B&C&\text{Minterns}&\text{Maxterms}&f&f’\\\hline 0&0&0&0&\text{A’B’C’}=\text{m}_0&\text{A+B+C}=\text{M}_0&0&1\\ 1&0&0&1&\text{A’B’C}=\text{m}_1&\text{A+B+C’}=\text{M}_1&0&1\\ 2&0&1&0&\text{A’BC’}=\text{m}_2&\text{A+B’+C}=\text{M}_2&0&1\\ 3&0&1&1&\text{A’BC}=\text{m}_3&\text{A+B’+C’}=\text{M}_3&1&0\\ 4&1&0&0&\text{AB’C’}=\text{m}_4&\text{A’+B+C}=\text{M}_4&1&0\\ 5&1&0&1&\text{AB’C}=\text{m}_5&\text{A’+B+C’}=\text{M}_5&1&0\\ 6&1&1&0&\text{ABC’}=\text{m}_6&\text{A’+B’+C}=\text{M}_6&1&0\\ 7&1&1&1&\text{ABC}=\text{m}_7&\text{A’+B’+C’}=\text{M}_7&1&0\\ \end{array} } \)

  • \(m_i’=M_i\)

  • \(\text{f=A’BC+A=1}\)
    \(\text{=A’BC+AB’C’+AB’C+ABC’+ABC}\)
    \(=m_3+m_4+m_5+m_6+m_7\)
    \(=\sum m(3,4,5,6,7)\)

  • \(\text{f=(A+B+C)(A+B+C’)(A+B’+C)=0}\)
    \(=M_0M_1M_2\)
    \(=\prod M(0,1,2)\)

  • Maxterm 與 minterm 的轉換
    \( \boxed{ \def\arraystretch{1}\begin{array}{rcl} g&=&\sum m(2,3,4,6,7)\\ &=&\prod M(0,1,5)\\ g’&=&\sum m(0,1,5)\\ g&=&[\sum m(0,1,5)]’\\ &=&\prod m’(0,1,5)\\ &=&\prod M(0,1,5) \end{array} } \)

  • 性質：

    • \(\boxed{\text{m}_i\text{m}_j=0\text{ if i}\neq j}\)

未完整定義的函式(Don’t Care)

  • Truth table:
    \( \boxed{ \def\arraystretch{1}\begin{array}{lll|l} A&B&C&F\\\hline 0&0&0&1\\ 0&0&1&X\leftarrow \text{Don’t care}\\ 0&1&0&0\\ 0&1&1&1\\ 1&0&0&0\\ 1&0&1&0\\ 1&1&0&X\leftarrow \text{Don’t care}\\ 1&1&1&1\\ \end{array} } \)
  • 表達式：
    • \(F=\sum m(0,3,7)+\sum d(1,6)=\prod M(2,4,5)\cdot \prod(1,6)\)

Binary adders and subtracters

Half Adder 半加器

  • \(X,Y_{\text{in}}\rightarrow{\boxed{\text{Half Adder}}\rightarrow \text{Sum}}\)
  • Truth Table:
    \( \boxed{ \def\arraystretch{1}\begin{array}{cc|c} X&Y&Sum\\\hline 0&0&0\\ 0&1&1\\ 1&0&1\\ 1&1&0\\ \end{array} } \)
  • 表達式： \(\text{Sum}=X’ Y+XY’\)

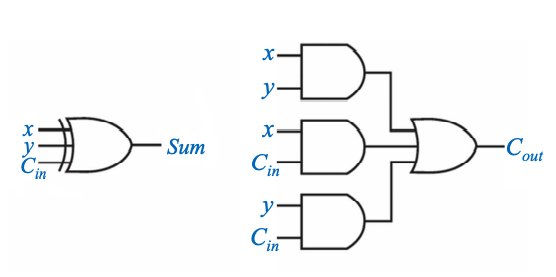
Full Adder 全加器

  • \(X,Y,C_{\text{in}}\rightarrow{\boxed{\text{Full Adder}}\rightarrow C_{out}, \text{Sum}}\)
  • Truth Table:
    \( \boxed{ \def\arraystretch{1}\begin{array}{ccc|cc} X&Y&C_{\text{in}}&C_{\text{out}}&\text{Sum}\\\hline 0&0&0&0&0\\ 0&0&1&0&1\\ 0&1&0&0&1\\ 0&1&1&1&0\\ 1&0&0&0&1\\ 1&0&1&1&0\\ 1&1&0&1&0\\ 1&1&1&1&1\\ \end{array} } \)
  • 表達式：
    • \(\text{Sum}=X\oplus Y\oplus C_{\text{in}}\)
    • \(C_\text{out}=YC_{\text{in}}+XC_{\text{in}}+XY\)
  • 邏輯電路 fulladder

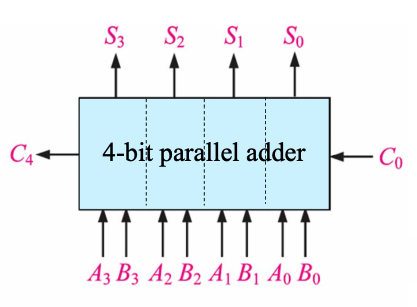
4-Bit Parallel Adder (Ripple Carry Adder 漣波加法器)

  • 四個平行串接的全加器 (Full Adder) 4bitadder

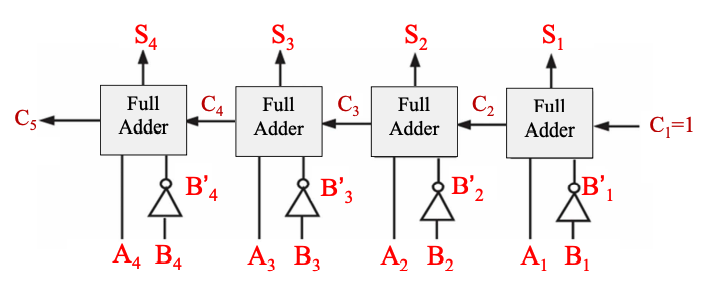
Binary Subtracter using Full Adders

  • 用全加器來實現減法器

subtracter

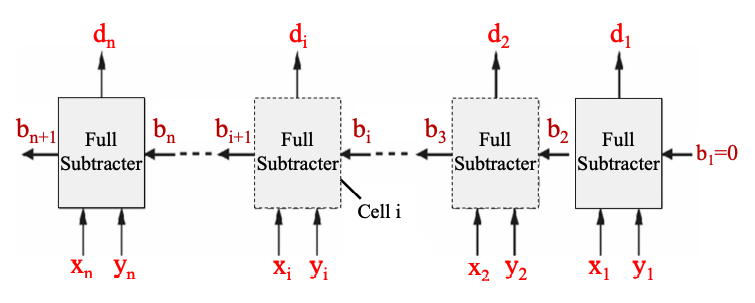
Full Subtracter

  • \(x_i,y_i,b_i\rightarrow\boxed{\text{Full Subtracter}}\rightarrow b_{i+1},d_i\)

  • Truth Table:
    \( \boxed{ \def\arraystretch{1}\begin{array}{ccc|cc} x_i&y_i&b_i&b_{i+1}&d_i\\\hline 0&0&0&0&0\\ 0&0&1&1&1\\ 0&1&0&1&1\\ 0&1&1&1&0\\ 1&0&0&0&1\\ 1&0&1&0&0\\ 1&1&0&0&0\\ 1&1&1&1&1\\ \end{array} } \)

  • 示意
    \( \boxed{ \def\arraystretch{1}\begin{array}{c|cc} &\text{Column i Before Borrow}&\text{Column i After Borrow}\\\hline x_i&0&10&\\ -b_i&-1&-1\\ -y_i&-1&-1\\\hline d_i&&0(b_{i+1}=1)\\ \end{array} } \)

Parallel Subtracter

subtracter2

Speeding up integer additions

Ripple Carry Adder

  • 一般的漣波進位加法器
    • 設計簡單、規律
    • 有較大的 Time Delay
      • 一個 Full Adder 為\(C_\text{out}=YC_{\text{in}}+XC_{\text{in}}+XY\)
      • 也就是先 AND 再 OR，兩個 gate delay
      • 故 n-bit adder 的 time delay 是 2n

Carry Lockahead Adder(CLA)

  • \(\text{Sum}=A\oplus B\oplus C_{in}\)
  • \(C_{out}=AB+(A+B)C_{in}\)
  • \(C_{i+1}=A_iB_i+(A_i+B_i)C_i\)
  • \(C_{i+1}=g_i+p_iC_i\)
    • \(g_i=A_iB_i\) generate function
    • \(p_i=A_i+B_i\) propagate function
  • \(C_2=g_1+p_1C_1\)
  • \(C_2=g_1+p_1p_0g_0+p_1p_0C_0\)
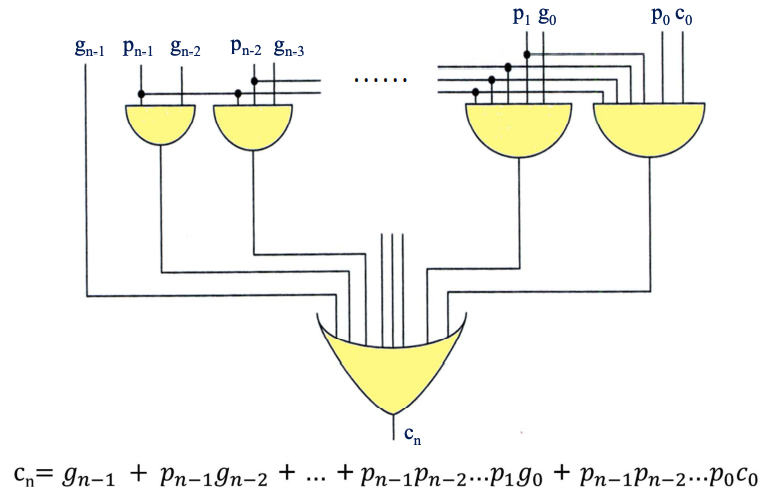
  • \(C_n=g_{n-1}+p_{n-1}g_{n-2}+p_{n-1}p_{n-2}g_{n-3}+…+p_{n-1}p_{n-2}…p_1g_0+p_{n-1}p_{n-2}…p_0C_0\)
  • 換句話說，\(C_n\)可以藉由 \(C_0\)運算出來，以 4-bit 為例，可以從漣波的 8 次降到 5 次的 Gate delay。 cla

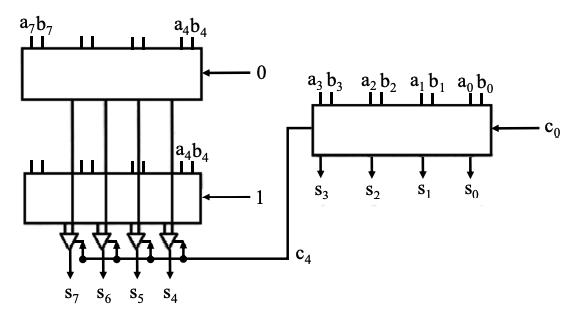
Carry Select Adder

  • 將兩個加法作平行處理
    • 預先假設 carry-in 的值，待前一級的 carry-in 算出後再用 selector 選擇正確的 carry-in，減去收到前級 carry-in 再開始運算的時間。 carryselector

Binary multiplication

  • 用邏輯閘模擬一般十進制進位法的乘法
    • 示意
      \( \def\arraystretch{1}\begin{array}{rcccc} \text{Multiplicand}&&&B_1&B_0\\ \text{Multiplier}&&&A_1&A_0\\\hline \text{Partial products}&&&A_0B_1&A_0B_0\\ \text{shift one bit left}&&A_1B_1&A_1B_0\\ \text{Sum of partial products}&C1&C2&C3&C4\\ \end{array} \)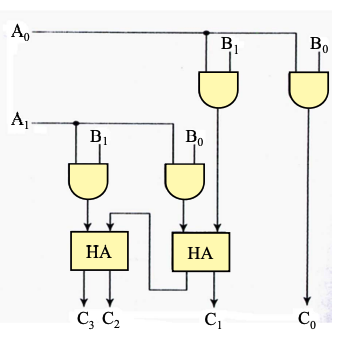 multiplication